题目内容
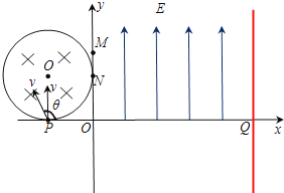
【题目】如图所示，在直角坐标系xoy的第一象限区域中，有沿y轴正方向的匀强电场，电场强度的大小为E=kv0。在第二象限有一半径为R=a的圆形区域磁场，圆形磁场的圆心O坐标为（﹣a，a），与坐标轴分别相切于P点和N点，磁场方向垂直纸面向里。在x=3a处垂直于x轴放置一平面荧光屏，与x轴交点为Q．大量的电子以相同的速率v0在纸面内从P点进入圆形磁场，电子的速度方向在与x轴正方向成θ角的范围内，其中沿y轴正方向的电子经过磁场到达N点，速度与x轴正方向成θ角的电子经过磁场到达M点，且M点坐标为（0，1.5a）．忽略电子间的相互作用力，不计电子的重力，电子的比荷为
。求：
（1）圆形磁场的磁感应强度大小；
（2）θ角的大小；
（3）电子打到荧光屏上距Q点的最远距离。
【答案】（1）k；（2）120°（3）
【解析】
（1）由于速度沿y轴正方向的电子经过N点，因而电子在磁场中做圆周运动的半径为：r=a
联立解得：
（2）电子在磁场中做圆周运动的圆心为O，电子离开磁场时的位置为P'，连接PO、P'O'可知该四边形为棱形，由于PO竖直，因而 半径P'O'也为竖直方向，电子离开磁场时速度一定沿x轴正方向．
由右图可知：
解得：
（3）由（2）可知，所有的电子以平行于x轴正方向的速度进入电场中做类似平抛运动，设电子在电场的运动时间为t，竖直方向位移为y，水平位移为x
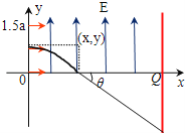
水平：
竖直：
联立解得：
设电子最终打在光屏的最远点距Q点为H，电子射出电场时的夹角为θ有：
又由：
当
时，即
时，H有最大值；
由于
，所以
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
