题目内容
15.“嫦娥四号”专家称“四号星”,计划在2017年发射升空,它是嫦娥探月工程计划中嫦娥系列的第四颗人造探月卫星,主要任务是更深层次、更加全面地科学探测月球地貌、资源等方面的信息,完善月球档案资料,已知月球的半径为R,月球表面的重力加速度为g,月球的平均密度为ρ,“嫦娥四号”离月球中心的距离为r,绕月周期为T,根据以上信息,下列说法正确的是( )| A. | 月球的第一宇宙速度为$\sqrt{gr}$ | B. | “嫦娥四号”绕月运行的速度为$\sqrt{\frac{g{R}^{2}}{r}}$ | ||
| C. | 万有引力常量可表示为$\frac{3π{r}^{3}}{ρ{T}^{2}{R}^{3}}$ | D. | 万有引力常量可表示为$\frac{3g}{4πRp}$ |
分析 1、根据重力提供向心力mg=m$\frac{v2}{R}$,得月球的第一宇宙速度为v=$\sqrt{gR}$.
2、根据万有引力提供向心力和月球表面的物体受到的重力等于万有引力,二式化简可得嫦娥四号的速度.
3、根据万有引力提供向心力得月球的质量M,解得月球的密度ρ=$\frac{M}{V}$,变形可得万有引力常量.
解答 解:A、重力提供向心力mg=m$\frac{v2}{R}$,得月球的第一宇宙速度为v=$\sqrt{gR}$.故A错误.
B、根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,得v=$\sqrt{\frac{GM}{r}}$,又因为月球表面的物体受到的重力等于万有引力G$\frac{Mm}{{R}^{2}}$=mg,得v=$\sqrt{\frac{g{R}^{2}}{r}}$,故B正确.
C、根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m($\frac{2π}{T}$)2r,
月球的密度ρ=$\frac{M}{V}$,所以万有引力常量为G=$\frac{3π{r}^{3}}{ρ{T}^{2}{R}^{3}}$.故C正确,D错误.
故选:BC
点评 解决本题的关键掌握万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$和月球表面的物体受到的重力等于万有引力G$\frac{Mm}{{R}^{2}}$=mg两个公式的综合应用,注意轨道半径与星体半径的关系.

练习册系列答案
相关题目
3.矩形线圈在匀强磁场中匀速转动产生的电动势如图示,则( )


| A. | t1时刻线圈中磁通量为零 | B. | t2时刻线圈中磁通量变化率最大 | ||
| C. | t3时刻线圈中磁通量变化率最大 | D. | t4时刻线圈面与磁场方向垂直 |
10.下列关于地球同步通讯卫星的说法中正确的是( )
| A. | 所有同步通讯卫星的周期都是24h | |
| B. | 所有同步通讯卫星必须定点在地球赤道上空某处 | |
| C. | 不同的同步通讯卫星的轨道半径一般是不同的 | |
| D. | 不同的同步通讯卫星运行的线速度大小是相同的,但加速度的大小可能不同 |
7. 如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )
如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )
 如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )
如图所示,平行板电容器充电后形成一个匀强电场,大小保持不变.让质子流以不同初速度,先、后两次垂直电场射入,分别沿a、b轨迹落到极板的中央和边缘,则质子沿b软迹运动时( )| A. | 初速度更大 | B. | 加速度更大 | ||
| C. | 动能增量更大 | D. | 两次的电势能增量相同 |
4.下列说法正确的是( )
| A. | 向心加速度是描述线速度变化快慢的物理量 | |
| B. | 圆周运动合外力完全充当向心力 | |
| C. | 向心力对物体永远不会做功 | |
| D. | 做匀速圆周运动的物体,向心力指向圆心,方向不变 |
 如图是“验证机械能守恒定律”的实验装置示意图.以下列出了一些实验步骤:
如图是“验证机械能守恒定律”的实验装置示意图.以下列出了一些实验步骤: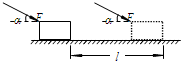 如图所示,质量为m的物块在与水平方向成α角的恒定推力F的作用下,由静止沿水平面向右运动一段距离l时,速度为v.在此过程中,恒力F对物块所做的功为Flcosα,重力做功为0,摩擦力做功为$\frac{1}{2}$mv2-Flcosα.速度为v时推力F的功率为Fvcosα.
如图所示,质量为m的物块在与水平方向成α角的恒定推力F的作用下,由静止沿水平面向右运动一段距离l时,速度为v.在此过程中,恒力F对物块所做的功为Flcosα,重力做功为0,摩擦力做功为$\frac{1}{2}$mv2-Flcosα.速度为v时推力F的功率为Fvcosα. 如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m,细线AC长l,B点距C点的水平距离和竖直距离相等.(cos37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m,细线AC长l,B点距C点的水平距离和竖直距离相等.(cos37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)