Question

A．B两辆汽车在笔直的公路上同向行驶。当 B车在A车前84 m处时，B车速度为4 m/s，且正以2 m/s²的加速度做匀加速运动；经过一段时间后，B车加速度突然变为零。A车一直以20 m/s的速度做匀速运动。经过12 s后两车相遇。问B车加速行驶的时间是多少？

Answer 1

、解：设A车的速度为v_A，B车加速行驶时间为t，两车在t₀时相遇。则有
X_A=v_At                                   ①
X_B=v_Bt+at²/2+(v_B+at)(t₀-t)              ②
式中，t₀ =12s，X_A．X_B分别为 A．B两车相遇前行驶的路程。依题意有
  X_A = X_B +X                             ③
式中 X＝84 m。由①②③式得
t²-2t₀t+ ="0                        " ④
代入题给数据
v_A=20m/s，v_B=4m/s，a =2m/s²，
有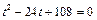 
                                           ⑤
式中矿的单位为s。解得
t₁="6" s，t₂="18" s                                         ⑥
t₂＝18s不合题意，舍去。因此，B车加速行驶的时间为 6 s。

解析