题目内容
9.在“验证机械能守恒定律”实验中:
(1)下列测量工具中必需的是C.
A.天平 B.弹簧测力计 C.刻度尺 D.秒表
(2)如图是实验中得到的一条纸带.已知打点计时器所用电源的频率为50Hz,当地重力加速度g=9.80m/s2,测得所用重物的质量为1.00kg,纸带上所打第一个点O与相邻第二个点之间的距离接近2mm,A、B、C、D是连续打出的四个点,它们到O点的距离分别为OA=71.71cm,OB=79.80cm,OC=87.95cm,OD=96.21cm.则由以上数据可知,重物运动到纸带打C点时的速度为4.1 m/s,重物从打O点运动到打C点的过程中,重物动能的增加量为8.4_ J,重力势能的减小量为8.6 J. (结果都保留两位有效数字)
(3)由此可得到的结论是在误差允许的范围内,重物机械能守恒.
分析 (1)根据实验的原理确定所需测量的物理量,从而确定必需的器材.
(2、3)根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的速度,从而得出动能的增加量,根据下降的高度求出重力势能的减小量,通过比较得出实验的结论.
解答 解:(1)实验中验证动能的增加量和重力势能的减小量是否相等,质量可以约去,不需要测量质量,则不需要天平、弹簧测力计,打点计时器可以记录时间,所以不需要秒表.实验中需用刻度尺测量点迹间的距离,从而求解瞬时速度以及下降的高度.故选:C.
(2)C点的瞬时速度${v}_{C}=\frac{{x}_{BD}}{2T}=\frac{(96.21-79.80)×1{0}^{-2}}{2×0.02}$m/s=4.1025m/s≈4.1m/s,则重物动能的增加量$△{E}_{k}=\frac{1}{2}m{{v}_{C}}^{2}$=$\frac{1}{2}×1×4.102{5}^{2}$=8.4J,重力势能的减小量为△Ep=mgh=1×9.8×87.95×10-2=8.6J.
(3)由此可知,在误差允许的范围内,重物机械能守恒.
故答案为:(1)C.(2)4.1,8.4,8.6,(3)在误差允许的范围内,重物机械能守恒.
点评 解决本题的关键知道实验的原理,掌握纸带的处理方法,会根据纸带求解瞬时速度,从而得出动能的增加量,会根据下降的高度求解重力势能的减小量.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
8.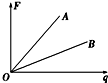 在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )
在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )
 在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )
在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )| A. | EA>EB | B. | EA<EB | ||
| C. | EA=EB | D. | 不能判定EA、EB的大小 |
17.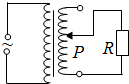 如图所示,理想变压器原线圈接入电压有效值恒定的正弦交流电,副线圈接一定值电阻R.调节触头P,使副线圈匝数变为原来的一半,则调节前后( )
如图所示,理想变压器原线圈接入电压有效值恒定的正弦交流电,副线圈接一定值电阻R.调节触头P,使副线圈匝数变为原来的一半,则调节前后( )
 如图所示,理想变压器原线圈接入电压有效值恒定的正弦交流电,副线圈接一定值电阻R.调节触头P,使副线圈匝数变为原来的一半,则调节前后( )
如图所示,理想变压器原线圈接入电压有效值恒定的正弦交流电,副线圈接一定值电阻R.调节触头P,使副线圈匝数变为原来的一半,则调节前后( )| A. | 原线圈中的电流之比为4:1 | B. | 副线圈中的电流之比为2:1 | ||
| C. | 变压器的输入功率之比为4:1 | D. | 变压器的输出功率之比为1:2 |
14.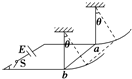 如图所示,水平放置的光滑平行金属导轨,左端通过开关S与内阻不计、电动势为E的电源相连,右端与半径为L=20cm的光滑圆弧导轨相接,导轨电阻均不计.导轨所在空间有竖直方向的匀强磁场,磁感应强度B=0.5T.一根质量m=60g、电阻R=1Ω、长为L的导体棒ab,用长也为L的绝缘细线悬挂,导体棒恰好与导轨接触.当闭合开关S后,导体棒沿圆弧摆动,摆动过程中导体棒始终与导轨接触良好且细线处于张紧状态,最后导体棒摆角最大时,细线与竖直方向的夹角θ=53°,sin 53°=0.8,g=10m/s2则( )
如图所示,水平放置的光滑平行金属导轨,左端通过开关S与内阻不计、电动势为E的电源相连,右端与半径为L=20cm的光滑圆弧导轨相接,导轨电阻均不计.导轨所在空间有竖直方向的匀强磁场,磁感应强度B=0.5T.一根质量m=60g、电阻R=1Ω、长为L的导体棒ab,用长也为L的绝缘细线悬挂,导体棒恰好与导轨接触.当闭合开关S后,导体棒沿圆弧摆动,摆动过程中导体棒始终与导轨接触良好且细线处于张紧状态,最后导体棒摆角最大时,细线与竖直方向的夹角θ=53°,sin 53°=0.8,g=10m/s2则( )
 如图所示,水平放置的光滑平行金属导轨,左端通过开关S与内阻不计、电动势为E的电源相连,右端与半径为L=20cm的光滑圆弧导轨相接,导轨电阻均不计.导轨所在空间有竖直方向的匀强磁场,磁感应强度B=0.5T.一根质量m=60g、电阻R=1Ω、长为L的导体棒ab,用长也为L的绝缘细线悬挂,导体棒恰好与导轨接触.当闭合开关S后,导体棒沿圆弧摆动,摆动过程中导体棒始终与导轨接触良好且细线处于张紧状态,最后导体棒摆角最大时,细线与竖直方向的夹角θ=53°,sin 53°=0.8,g=10m/s2则( )
如图所示,水平放置的光滑平行金属导轨,左端通过开关S与内阻不计、电动势为E的电源相连,右端与半径为L=20cm的光滑圆弧导轨相接,导轨电阻均不计.导轨所在空间有竖直方向的匀强磁场,磁感应强度B=0.5T.一根质量m=60g、电阻R=1Ω、长为L的导体棒ab,用长也为L的绝缘细线悬挂,导体棒恰好与导轨接触.当闭合开关S后,导体棒沿圆弧摆动,摆动过程中导体棒始终与导轨接触良好且细线处于张紧状态,最后导体棒摆角最大时,细线与竖直方向的夹角θ=53°,sin 53°=0.8,g=10m/s2则( )| A. | 磁场方向一定竖直向上 | |
| B. | 电源电动势E=8.0 V | |
| C. | 导体棒在摆动过程中所受安培力F=8 N | |
| D. | 导体棒在摆动过程中电源提供的电能为0.048J |
1.“神舟”七号进入轨道绕地球匀速圆周运动后,飞船内的物体处于“漂浮”状态,下列说法正确的是( )
| A. | 宇航员不再受重力作用 | |
| B. | 宇航员处于平衡状态 | |
| C. | 宇航员的加速度小于9.8m/s2 | |
| D. | 由于完全失重导致飞船容器内的气体压强等于零 |
19. 一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )
一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )
 一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )
一物体沿直线运动,其v-t图象如图所示,则关于该物体的运动情况,下述正确的是( )| A. | 第1s末物体的位移和速度都改变方向 | |
| B. | 前4s内物体的位移为零 | |
| C. | 第2s末物体的位移和速度都改变方向 | |
| D. | 第1s末、第3s末、第5s末物体所在的位置相同 |
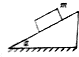 质量为m的物体,静止于一个倾角为α的斜面上,如图所示,如果已知物体所受重力和斜面对物体的弹力的合力方向平行于斜面向下,则这两个力的合力大小为mgsinα,斜面对物体的弹力大小为mgcosα,斜面对物体施加的摩擦力大小为mgsinα,方向平行于斜面向上.
质量为m的物体,静止于一个倾角为α的斜面上,如图所示,如果已知物体所受重力和斜面对物体的弹力的合力方向平行于斜面向下,则这两个力的合力大小为mgsinα,斜面对物体的弹力大小为mgcosα,斜面对物体施加的摩擦力大小为mgsinα,方向平行于斜面向上.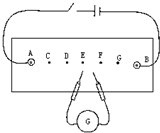 如图是描绘电场中等势线的实验装置,图中有7个等间距的点,其中A、B为金属电极,当电流从标有“+”号的接线柱流入灵敏电流计G时,其指针正向偏转,则当灵敏电流计指针不偏时,探针所接触的两点恰是等势点;当探针1接在F点时,探针2应在F点的正上方或者正下方的某个位置往右移,才能找到等势点.
如图是描绘电场中等势线的实验装置,图中有7个等间距的点,其中A、B为金属电极,当电流从标有“+”号的接线柱流入灵敏电流计G时,其指针正向偏转,则当灵敏电流计指针不偏时,探针所接触的两点恰是等势点;当探针1接在F点时,探针2应在F点的正上方或者正下方的某个位置往右移,才能找到等势点.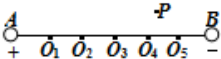 在用平面电流场模拟静电场来描绘电场等势线的实验中,因实验中灵敏电流计数量不够,某同学用电压表(所选量程适中)替代灵敏电流计来做实验.实验中所用直流电源电压的正、负极分别接在图中的A、B两点.A、B间有5个等分点Ol、O2、O3、O4、O5,作为对应电势的基准点.实验中,为描述通过基准点O4的等势线,可以将跟电压表正接线柱相连的探针甲接A点(填“A”或“B”),跟电压表负接线柱相连的探针乙接O4点,测出电压值U4=4V之后,在AB的上下区域用探针乙(填“甲”或“乙”)寻找O4的等势点;寻找中,该探针触到P点时,符合要求,则此时测得的电压值UP=4V((填“>”、“=”或“<”)
在用平面电流场模拟静电场来描绘电场等势线的实验中,因实验中灵敏电流计数量不够,某同学用电压表(所选量程适中)替代灵敏电流计来做实验.实验中所用直流电源电压的正、负极分别接在图中的A、B两点.A、B间有5个等分点Ol、O2、O3、O4、O5,作为对应电势的基准点.实验中,为描述通过基准点O4的等势线,可以将跟电压表正接线柱相连的探针甲接A点(填“A”或“B”),跟电压表负接线柱相连的探针乙接O4点,测出电压值U4=4V之后,在AB的上下区域用探针乙(填“甲”或“乙”)寻找O4的等势点;寻找中,该探针触到P点时,符合要求,则此时测得的电压值UP=4V((填“>”、“=”或“<”)