题目内容
8. 如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送 带速度相同,然后经A点沿半圆轨道滑下,且在B点对轨道的压力大小为10mg,再经B点滑上滑板,滑板运动到C点时被牢固粘连.物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离为L=2.5R,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数相同,重力加速度为g.求:
如图所示,以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑的地面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C两点,一物块(视为质点)被轻放在水平匀速运动的传送带上E点,运动到A点时刚好与传送 带速度相同,然后经A点沿半圆轨道滑下,且在B点对轨道的压力大小为10mg,再经B点滑上滑板,滑板运动到C点时被牢固粘连.物块可视为质点,质量为m,滑板质量为M=2m,两半圆半径均为R,板长l=6.5R,板右端到C点的距离为L=2.5R,E点距A点的距离s=5R,物块与传送带、物块与滑板间的动摩擦因数相同,重力加速度为g.求:(1)物块滑到B点的速度大小.
(2)物块与传送带、物块与滑板间的动摩擦因数.
(3)求物块与滑板间因摩擦而产生的总热量.
分析 (1)在B点,由轨道的支持力和重力的合力提供向心力,根据向心力公式求解;
(2)从E到B的过程中,根据动能定理求解;
(3)滑块滑上木板后做匀减速直线运动,木板做匀加速直线运动,根据牛顿第二定律求解加速度,根据运动学基本公式判断速度相当时的位置关系,再根据摩擦力做功公式结合能量守恒求解.
解答 解:(1)在B点,由轨道的支持力和重力的合力提供向心力,则有:
10mg-mg=m$\frac{{{v}_{B}}^{2}}{R}$
解得:${v}_{B}=3\sqrt{gR}$
(2)从E到B的过程中,根据动能定理得:
mg•2R+$μmgs=\frac{1}{2}m{{v}_{B}}^{2}$
解得:μ=0.5
(3)滑块滑上木板后做匀减速直线运动,木板做匀加速直线运动,
对物块由牛顿第二定律得:a1=$\frac{μmg}{m}=5m/{s}^{2}$
对滑板由牛顿第二定律得:a2=$\frac{μmg}{M}=2.5m/{s}^{2}$
设经过时间t滑板与物块达到共同速度v时,位移分别为x1、x2,
vB-a1t=a2t
${x}_{1}={v}_{B}t-\frac{1}{2}{a}_{1}{t}^{2}$
x2=$\frac{1}{2}{a}_{2}{t}^{2}$
联立解得:x1=2R,x2=8R
即物块与滑板在达到共同速度时,物块未离开滑板
则Q1=μmg(x2-x1)
物块与木板此后以共同速度匀速运动至C点 滑板则不再运动,物块继续往前运动0.5R冲上圆弧,
Q2=μmg•0.5R
物块滑回来,由能量守恒可得
Q3=$\frac{1}{2}m{v}^{2}$
则总热量Q=Q1+Q2+Q3=3.5mgR
答:(1)物块滑到B点的速度大小为$3\sqrt{gR}$.
(2)物块与传送带、物块与滑板间的动摩擦因数为0.5;
(3)求物块与滑板间因摩擦而产生的总热量位3.5mgR.
点评 本题考查机械能守恒以及有摩擦的板块模型中克服摩擦力做的功.判断物块与滑板在达到相同共同速度时,物块未离开滑板是关键,是一道比较困难的好题.

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案 如图,是我们家庭播放影片文件等常用的DVD光盘,光盘上的A、B两点距离圆心的距离不等,则当光盘匀速运动时,A、B两点的线速度( )
如图,是我们家庭播放影片文件等常用的DVD光盘,光盘上的A、B两点距离圆心的距离不等,则当光盘匀速运动时,A、B两点的线速度( )| A. | 大小不等,方向不同 | B. | 大小相等,方向不同 | ||
| C. | 大小不等,方向相同 | D. | 大小相等,方向相同 |
| A. | 经典力学在宏观低速运动中,引力不太大时适用 | |
| B. | 经典力学在今天广泛应用,它的正确性无可怀疑,仍是普遍适用的 | |
| C. | 经典力学在历史上起了巨大的作用,随着物理学的发展而逐渐过时,成为一种古老的理论 | |
| D. | 由于相对论、量子论的提出,经典力学已经失去了它的意义 |
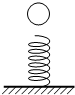 如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )| A. | 小球的机械能守恒 | |
| B. | 重力势能和弹性势能之和先减小后增加 | |
| C. | 动能和弹性势能之和先减小后增加 | |
| D. | 重力势能与动能之和始终增大 |
| A. | 甲的周期大于乙的周期 | B. | 甲的加速度大于乙的加速度 | ||
| C. | 乙的速度大于第一宇宙速度 | D. | 甲的向心力大于乙的向心力 |
 如图为某台电风扇的铭牌,如果已知该电风扇在额定电压下工作时,转化为机械能的功率等于电动机消耗电功率的97%,则在额定电压下工作时,通过电动机的电流I及电动机线圈的电阻R分别是( )
如图为某台电风扇的铭牌,如果已知该电风扇在额定电压下工作时,转化为机械能的功率等于电动机消耗电功率的97%,则在额定电压下工作时,通过电动机的电流I及电动机线圈的电阻R分别是( )| A. | I=0.3A,R=711Ω | B. | I=0.3A,R=22Ω | C. | I=3.3A,R=711Ω | D. | I=3.3A,R=22Ω |
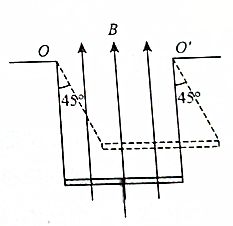 如图所示,质量为60g的导体棒长度S=20cm,棒两端分别与长度L=30cm的细导线相连,悬挂在竖直向上的匀强磁场中,磁感应强度B=0.5T.当导体棒中通以稳恒电流I后,棒向上摆动(摆动过程中I始终不变),最大偏角θ=45°,求:导体棒中电流I的大小.(可用根式表示)
如图所示,质量为60g的导体棒长度S=20cm,棒两端分别与长度L=30cm的细导线相连,悬挂在竖直向上的匀强磁场中,磁感应强度B=0.5T.当导体棒中通以稳恒电流I后,棒向上摆动(摆动过程中I始终不变),最大偏角θ=45°,求:导体棒中电流I的大小.(可用根式表示)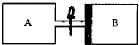 如图所示,导热材料制成的截面积相等,长度均为L=45cm的气缸A、B通过带有阀门的管道连接,初始时阀门K关闭,厚度不计的质量为m=24kg,面积S=20cm2光滑活塞C位于B内下侧,在A内充满压强PA=2×105Pa的理想气体,B内充满压强PB=1×105Pa的同种理想气体,忽略连接气缸的管道体积,室温不变,现打开阀门,求最终平衡时活塞向上移动的距离?
如图所示,导热材料制成的截面积相等,长度均为L=45cm的气缸A、B通过带有阀门的管道连接,初始时阀门K关闭,厚度不计的质量为m=24kg,面积S=20cm2光滑活塞C位于B内下侧,在A内充满压强PA=2×105Pa的理想气体,B内充满压强PB=1×105Pa的同种理想气体,忽略连接气缸的管道体积,室温不变,现打开阀门,求最终平衡时活塞向上移动的距离?