题目内容
17. 将一个物体以10m/s的初速度从30m高处水平抛出,不计空气阻力,建立如图所示坐标系,(g取10m/s2),求:
将一个物体以10m/s的初速度从30m高处水平抛出,不计空气阻力,建立如图所示坐标系,(g取10m/s2),求:(1)它抛出2s后所在位置的坐标和速度大小?
(2)该物体在空中运动的轨迹方程?
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出平抛运动的时间,判断物体是否落地,再结合运动学公式分析求解.
解答 解:(1)物体落地的时间为:
t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×30}{10}}s=\sqrt{6}s>2s$,
则2s时水平位移为:x=v0t=10×2m=20m,
竖直位移为:y=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×4m=20m$,
可知抛出2s后位置坐标为(20m,20m).
2s末竖直分速度为:vy=gt=10×2m/s=20m/s,
根据平行四边形定则知,速度的大小为:
v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{100+400}m/s=10\sqrt{5}$m/s.
(2)根据x=v0t=10t,y=$\frac{1}{2}g{t}^{2}=5{t}^{2}$
得:y=$\frac{{x}^{2}}{20}$m.
答:(1)它抛出2s后所在位置的坐标为(20m.20m),速度大小$10\sqrt{5}$m/s.
(2)物体在空中的轨迹方程为y=$\frac{{x}^{2}}{20}$m.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
8.人造卫星在地面附近绕地球做匀速圆周运动所必须具有的速度,称为第一宇宙速度.第一宇宙速度大小是( )
| A. | 11.2km/s | B. | 7.9km/s | C. | 16.7km/s | D. | 光速 |
12.如图所示,在一楼梯上移动一个质量为m的小球,选第2级台阶为零势能面,每级台阶的高度为h,则( )


| A. | 小球在第1级台阶时的重力势能为:mgh | |
| B. | 小球从第1级移至第3级时,重力势能变化量为:-2mgh | |
| C. | 小球从第1级移至第3级时,重力做功为:2mgh | |
| D. | 小球的重力势能变化与参考面的位置无关 |
2.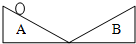 如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
 如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )
如图为理想的实验模型,如果空气阻力和摩擦力小到可以忽略,小球必将准确的终止于它开始运动时的高度,不会更高一点,也不会更低一点,这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是( )| A. | 高度 | B. | 动能 | C. | 势能 | D. | 能量 |
9.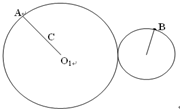 图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
 图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )
图中A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动.则正确的有( )| A. | A、B两点的角速度大小跟半径成反比 | |
| B. | A、B两点的角速度大小跟半径成正比 | |
| C. | A、C两点的线速度大小跟半径成反比 | |
| D. | A、C两点的线速度大小跟半径成正比 |
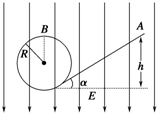 如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α,圆轨道半径为R,小球的重力大于受的电场力.
如图所示,在竖直向下的匀强电场中有一绝缘的光滑轨道,一个带负电的小球从斜轨上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电荷量为-q,匀强电场的场强大小为E,斜轨道的倾角为α,圆轨道半径为R,小球的重力大于受的电场力.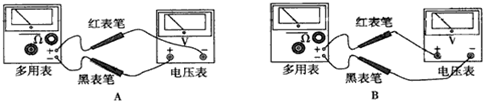

 如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )
如图甲所示,在列车首节车厢下面安装一电磁铁,电磁铁产生垂直于地面的匀强磁场,首节车厢经过安放在两铁轨间的线圈时,线圈产生的电脉冲信号传到控制中心.图乙为某时控制中心显示屏上的电脉冲信号,则此时列车的运动情况是( )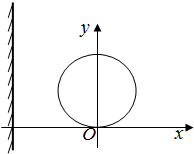 如图所示,x轴正方向水平向右,y轴正方向竖直向上.在xoy平面内有与y轴平行的匀强电场,在圆心为C半径为R的圆内还有与xoy平面垂直的匀强磁场.在原点O放置一带电微粒发射装置,它发射出质量为m、电荷量为q(q>0)和初速度大小为v的同种带电微粒,速度方向分布在xoy平面第一和第二象限内的各个方向上.已知从O点沿y轴正方向发射的带电微粒射出磁场区域后平行于x轴运动.在x轴上有一与y轴平行的荧光屏.重力加速度为g.
如图所示,x轴正方向水平向右,y轴正方向竖直向上.在xoy平面内有与y轴平行的匀强电场,在圆心为C半径为R的圆内还有与xoy平面垂直的匀强磁场.在原点O放置一带电微粒发射装置,它发射出质量为m、电荷量为q(q>0)和初速度大小为v的同种带电微粒,速度方向分布在xoy平面第一和第二象限内的各个方向上.已知从O点沿y轴正方向发射的带电微粒射出磁场区域后平行于x轴运动.在x轴上有一与y轴平行的荧光屏.重力加速度为g.