Question

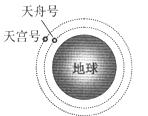
【题目】如图，粗细均匀、两端开口的U形管竖直放置，两管的竖直部分高度为20cm，内径很小，水平部分BC长14cm．一空气柱将管内水银分隔成左右两段．大气压强P0=76cmHg．当空气柱温度为T0=273K、长为L0=8cm时，BC管内左边水银柱长2cm，AB管内水银柱长也为2cm．求：

（1）右边水银柱总长是多少？

（2）当空气柱温度升高到多少时，左边的水银恰好全部进入竖直管AB内？

（3）为使左、右侧竖直管内的水银柱上表面高度差最大，空气柱温度至少要升高到多少？

Answer 1

【答案】（1）6cm （2）420K （3）980K

【解析】试题分析：由于平衡，两边水银面等高，即可求得右边水银柱总长；左边的水银恰好全部进入竖直管AB内时，根据左侧水银柱平衡可以求出底部气体的压强，然后根据玻意耳定律列式求解；当AB管中水银柱上表面恰好上升到管口时，高度差最大，封闭气体发生等压变化，根据盖吕萨克定律求解空气柱温度。

（1）由于水银柱处于平衡状态，则有 P1=P0+h左=P0+h右

带入数据解得：h右=2cm，

可得右边水银柱总长为：L右=h右+4cm=6cm

（2）当左边水银全部进入AB管时，右边竖直管中水银柱高也为4cm

此时气体压强为P2=80cmHg，空气柱长度L2=（8+2+2）cm=12cm

初态：P1=78cmHg L1=8cm T0=273K

由理想气体状态方程得：

带入数据解得：T2=420K

（3）当AB管中水银柱上表面恰好上升到管口时，高度差最大．此时右边有2cm长的水银柱停在管的水平部分，则空气柱总长为L3=（20﹣4）cm+（14﹣2）cm=28cm．

因封闭气体发生等压变化，则有

带入数据解得：T3=980K