Question

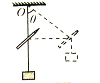
【题目】如图所示，轻杆的一端用铰链固定在竖直转轴OO′上的O端，另一端固定一小球，轻杆可在竖直平面内自由转动，当转轴以某一角速度匀速转动时，小球在水平面内做匀速圆周转动，此时轻杆与竖直转轴OO′的夹角为37°．已知转轴O端距离水平地面的高度为h，轻杆长度为L，小球的质量为m，重力加速度为g，取sin37°≈0.6，cos37°≈0.8，求：

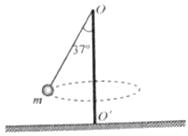
（1）小球做匀速圆周运动的线速度v．

（2）若某时刻小球从轻杆上脱落，小球的落地点到转轴的水平距离d．

（3）若缓慢增大转轴的转速，求轻杆与转轴的夹角从37°增加到53°的过程中，轻杆对小球所做的功W．

Answer 1

【答案】（1）小球做匀速圆周运动的线速度v为．

（2）若某时刻小球从轻杆上脱落，小球的落地点到转轴的水平距离d为．

（3）轻杆对小球所做的功为．

【解析】

（1）小球在水平面做匀速圆周运动，根据牛顿第二定律得：

mgtan

解得：v=

（2）小球从轻杆上脱落后做平抛运动，

根据平抛运动的规律有：h﹣Lcosθ=

水平位移x=vt

根据几何关系有：d2=x2+（Lsinθ）2

解得：d=

（3）设夹角增加到53°时，小球的速度为v′，则

由动能定理得：

W﹣mgL（cos37°﹣cos53°）=

解得：W=

答：（1）小球做匀速圆周运动的线速度v为．

（2）若某时刻小球从轻杆上脱落，小球的落地点到转轴的水平距离d为．

（3）轻杆对小球所做的功为．