Question

【题目】如图所示，ABCD是一直角梯形棱镜的横截面，位于截面所在平面内的一束光线由O点垂直AD边射入．已知棱镜的折射率n= ，AB=BC=8cm，OA=2cm，∠OAB=60°．

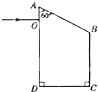
①求光线第一次射出棱镜时，出射光线的方向？
②第一次的出射点距C点多远？

Answer 1

【答案】解：①因为sinC= ，临界角C=45°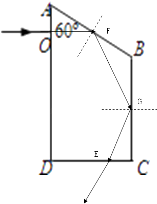

第一次射到AB面上的入射角为60°，大于临界角，所以发生全发射，反射到BC面上，入射角为60°，又发生全反射，射到CD面上的入射角为30°
根据折射定律得，n= ，
解得θ=45°．
即光从CD边射出，与CD边成45°斜向左下方．
②根据几何关系得，AF=4cm，则BF=4cm．
∠BFG=∠BGF，则BG=4cm．所以GC=4cm．
所以CE= cm．
答：①从CD边射出，与CD边成45°斜向左下方
②第一次的出射点距 cm．
【解析】①根据sinC= ，求出临界角的大小，从而作出光路图，根据几何关系，结合折射定律求出出射光线的方向．②根据几何关系，求出第一次的出射点距C的距离．