Question

【题目】如图所示为六根与水平面平行的导线的横截面示意图，导线分布在正六边形的六个角，导线所通电流方向已在图中标出。已知每条导线在O点磁感应强度大小为，则正六边形中心O处磁感应强度的大小和方向（　　）

A.大小为零

B.大小，方向沿轴负方向

C.大小，方向沿轴正方向

D.大小，方向沿y轴正方向

Answer 1

【答案】D

【解析】

根据磁场的叠加原理，将最右面电流向里的导线在O点产生的磁场与最左面电流向外的导线在O点产生的磁场进行合成，则这两根导线的合磁感应强度为B1；

同理，将左上方电流向外的导线在O点产生的磁场与右下方电流向里的导线在O点产生的磁场进行合成，则这两根导线的合磁感应强度为B2；

将右上方电流向里的导线在O点产生的磁场与左下方电流向外的导线在O点产生的磁场进行合成，则这两根导线的合磁感应强度为B3。

如图所示：

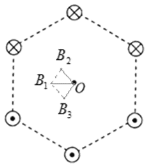
根据磁场叠加原理可知

由几何关系可知B2与B3的夹角为120°，故将B2与B3合成，则它们的合磁感应强度大小也为2B0，方向与B1的方向相同，最后将其与B1合成，可得正六边形中心处磁感应强度大小为4 B0，方向沿y轴正方向.

选项D正确，ABC错误。

故选D。