题目内容
19.如图所示,MN、PQ是相互平行的足够长的直导轨,与水平面成37°角倾斜放置,其间距l=0.2m,R1、R2是连在导轨两端的电阻,R1=R2=0.8Ω,ab是跨接在导轨上质量m=0.1kg,长度L=0.3m的粗细均匀的导体棒,导体棒的总电阻r=0.3Ω,空间存在B=0.5T,方向斜向上与斜面轨道垂直的匀强磁场,如图1所示,从零时刻开始,通过微型电动机对ab棒施加一个牵引力F,沿斜面轨道平行向上,使其从静止开始沿导轨做加速运动,2s末牵引力F的功率是2.64W,此过程中导体棒始终保持与导轨垂直且接触良好,图2是棒3s内的速度-时间图象,除R1、R2及导体棒的总电阻以外,其余部分的电阻均不及,g=10m/s2.
(1)求导体棒与导轨间的动摩擦因数;
(2)如果牵引力F从静止起作用3s后突然变为大小为0.73N的恒力,方向不变,求这之后电阻R1消耗的最小功率.
分析 (1)根据图象2求出金属棒的加速度,再对t=2s时根据牛顿第二定律列式求解;
(2)如果牵引力F从静止起作用3s后突然变为大小为0.73N的恒力,方向不变,之后金属棒做加速度减小的减速运动,当加速度为零后匀速直线运动,在此过程中匀速运动的速度为最小速度,此时电阻R1消耗的功率最小,根据功率公式和闭合电路欧姆定律、受力平衡列式求解即可.
解答 解:(1)由图2得金属棒的加速度为:$a=\frac{△v}{△t}=\frac{3}{2}m/{s}^{2}=1.5m/{s}^{2}$,
2s末金属棒的速度为3m/s,牵引力F的功率是2.64W,根据P=Fv得:
2s末金属棒受到的外力为:${F}_{1}=\frac{P}{v}=\frac{2.64}{3}N=0.88N$ ①
由牛顿第二定律得:F1-mgsin37°-BIl-μmgcos37°=ma ②
由闭合电路欧姆定律得:$I=\frac{E}{R+r}$ ③
其中$R=\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$ E=Blv④
①②③④联立解得:μ=0.04 ⑤
(2)牵引力F从静止起作用3s后突然变为大小为0.73N的恒力后金属棒做减速运动,当加速度为零时速度最小
根据平衡得:F2-mgsin37°-BI′l-μmgcos37°=0 ⑥
电阻R1消耗的最小功率为:${P}_{{R}_{1}}=(\frac{1}{2}I′)^{2}{R}_{1}$ ⑦
⑤⑥⑦联立求解得:${P}_{{R}_{1}}=0.09W$
答:(1)求导体棒与导轨间的动摩擦因数为0.04;
(2)电阻R1消耗的最小功率为0.09W.
点评 本题考查闭合电路欧姆定律与安培力的结合,要注意正确作出受力分析,根据共点力的平衡和牛顿第二定律列式求解.

 如图所示,圆弧形轨道上,上表面光滑,下表面也光滑,有一个质量为m的小物体从圆弧轨道上表面滑过,到达圆弧轨道竖直方向最高点时,对轨道的压力为物块重力的一半,速度大小为v1,若小物块从圆弧下表面滑过轨道,到达轨道竖直方向最高点时,对轨道的压力为物体的重力的一半,速度大小为v2,不计轨道的厚度,则$\frac{{v}_{1}}{{v}_{2}}$等于( )
如图所示,圆弧形轨道上,上表面光滑,下表面也光滑,有一个质量为m的小物体从圆弧轨道上表面滑过,到达圆弧轨道竖直方向最高点时,对轨道的压力为物块重力的一半,速度大小为v1,若小物块从圆弧下表面滑过轨道,到达轨道竖直方向最高点时,对轨道的压力为物体的重力的一半,速度大小为v2,不计轨道的厚度,则$\frac{{v}_{1}}{{v}_{2}}$等于( )| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}$:1 | C. | 1:2 | D. | 2:1 |
 如图所示,斜面体A放在粗糙水平地面上,用轻绳拴住的小球B置于斜面上,整个系统处于静止状态,已知斜面倾角及轻绳与竖直方向夹角均为θ=30°.现将斜面体A水平向右推动少许,整个系统仍处于静止状态,不计小球与斜面间的摩擦.则( )
如图所示,斜面体A放在粗糙水平地面上,用轻绳拴住的小球B置于斜面上,整个系统处于静止状态,已知斜面倾角及轻绳与竖直方向夹角均为θ=30°.现将斜面体A水平向右推动少许,整个系统仍处于静止状态,不计小球与斜面间的摩擦.则( )| A. | 地面对斜面体存在水平向右的静摩擦力 | |
| B. | 斜面体对地面的压力变大 | |
| C. | 轻绳对小球的拉力变大 | |
| D. | 斜面体对小球的支持力变大 |
| A. | 电场强度 | B. | 功 | C. | 加速度 | D. | 力 |
 如图所示是某次利用气垫导轨探究加速度与力、质量关系,在装置安装完毕后、闭合电路开关前的示意图.图中A为沙桶和沙,B为定滑轮,C为滑块及上面添加的砝码,D为纸带,E为电火花计时器,F为蓄电池(电动势为6V),S为开关,请指出图中的三处错误:
如图所示是某次利用气垫导轨探究加速度与力、质量关系,在装置安装完毕后、闭合电路开关前的示意图.图中A为沙桶和沙,B为定滑轮,C为滑块及上面添加的砝码,D为纸带,E为电火花计时器,F为蓄电池(电动势为6V),S为开关,请指出图中的三处错误: 如图所示是用激光器、缝间距可调节的双缝屏、光屏等器材研究光的干涉现象的装置.
如图所示是用激光器、缝间距可调节的双缝屏、光屏等器材研究光的干涉现象的装置.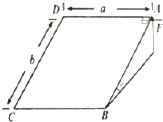 如图所示,粗糙斜面倾角θ=37°,斜面宽a为3m,长b为4m,质量为0.1kg的小木块从斜面A点静止释放,释放同时用与斜面底边BC平行的恒力F推该小木块,小木块与斜面间的动摩擦因数为μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8).
如图所示,粗糙斜面倾角θ=37°,斜面宽a为3m,长b为4m,质量为0.1kg的小木块从斜面A点静止释放,释放同时用与斜面底边BC平行的恒力F推该小木块,小木块与斜面间的动摩擦因数为μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8). 将一光滑斜面体放在水平面上,现将质量相同的滑块甲、乙由斜面体顶端释放,两物体沿斜面下滑过程中斜面始终保持静止,已知斜面体质量M,两滑块质量为m,重力加速度g,求下滑过程水平面所受压力.
将一光滑斜面体放在水平面上,现将质量相同的滑块甲、乙由斜面体顶端释放,两物体沿斜面下滑过程中斜面始终保持静止,已知斜面体质量M,两滑块质量为m,重力加速度g,求下滑过程水平面所受压力.