题目内容
两块足够大的平行金属极板水平放置,极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向)。在t=0时刻由负极板释放一个初速度为零的带负电的粒子(不计重力)。若电场强度E0、磁感应强度B0、粒子的比荷![]() 均已知,且
均已知,且![]() ,两板间距
,两板间距![]() 。
。
(1)求粒子在0~t0时间内的位移大小与极板间距h的比值。
(2)求粒子在板板间做圆周运动的最大半径(用h表示)。
(3)若板间电场强度E随时间的变化仍如图1所示,磁场的变化改为如图3所示,试画出粒子在板间运动的轨迹图(不必写计算过程)。

解析:
解法一:(1)设粒子在0~t0时间内运动的位移大小为s1
![]() ①
①
![]() ②
②
又已知![]()
联立①②式解得
![]() ③
③
(2)粒子在t0~2t0时间内只受洛伦兹力作用,且速度与磁场方向垂直,所以粒子做匀速圆周运动。设运动速度大小为v1,轨道半径为R1,周期为T,则
![]() ④
④
![]() ⑤
⑤
联立④⑤式得
![]() ⑥
⑥
又![]() ⑦
⑦
即粒子在t0~2t0时间内恰好完成一个周期的圆周运动。在2t0~3t0时间内,粒子做初速度为v1的匀加速直线运动,设位移大小为s2
![]() ⑧
⑧
解得 ![]() ⑨
⑨
由于s1+s2<h,所以粒子在3t0~4t0时间内继续做匀速圆周运动,设速度大小为v2,半径为R2
![]() ⑩
⑩
![]() 11
11
解得 ![]() 12
12
由于s1+s2+R2<h,粒子恰好又完成一个周期的圆周运动。在4t0~5t0时间内,粒子运动到正极板(如图1所示)。因此粒子运动的最大半径![]() 。
。

(3)粒子在板间运动的轨迹如图2所示。
解法二:由题意可知,电磁场的周期为2t0,前半周期粒子受电场作用做匀加速直线运动,加速度大小为
![]() 方向向上
方向向上
后半周期粒子受磁场作用做匀速圆周运动,周期为T
![]()
粒子恰好完成一次匀速圆周运动。至第n个周期末,粒子位移大小为sn
![]()
又已知 ![]()
由以上各式得 ![]()
粒子速度大小为 ![]()
粒子做圆周运动的半径为 ![]()
解得 ![]()
显然 ![]()
(1)粒子在0~t0时间内的位移大小与极板间距h的比值 ![]()
(2)粒子在极板间做圆周运动的最大半径 ![]()
(3)粒子在板间运动的轨迹图见解法一中的图2。

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案 如图所示,A、B为两块足够大的平行金属板,两板间距离为d,接在电压为U的电源上.在A板的中央P点处放置一个电子放射源,可以向各个方向释放电子.设电子的质量为m、电荷量为e,射出的初速度为v.求电子打在B板上的区域面积.
如图所示,A、B为两块足够大的平行金属板,两板间距离为d,接在电压为U的电源上.在A板的中央P点处放置一个电子放射源,可以向各个方向释放电子.设电子的质量为m、电荷量为e,射出的初速度为v.求电子打在B板上的区域面积.
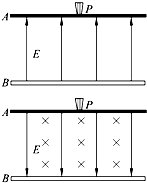 静电喷漆技术具有效率高、质量好、有益于健康等优点,其装置可简化如图.A、B为水平放置的间距d=0.9m的两块足够大的平行金属板,两板间有方向由B指向A的匀强电场,电场强度为E=0.1V/m.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小均为v0=8m/s的油漆微粒,已知油漆微粒的质量均为m=1×10-5 kg、电荷量均为q=-1×10-3 C不计空气阻力,油漆微粒最后都能落在金属板B上.
静电喷漆技术具有效率高、质量好、有益于健康等优点,其装置可简化如图.A、B为水平放置的间距d=0.9m的两块足够大的平行金属板,两板间有方向由B指向A的匀强电场,电场强度为E=0.1V/m.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小均为v0=8m/s的油漆微粒,已知油漆微粒的质量均为m=1×10-5 kg、电荷量均为q=-1×10-3 C不计空气阻力,油漆微粒最后都能落在金属板B上.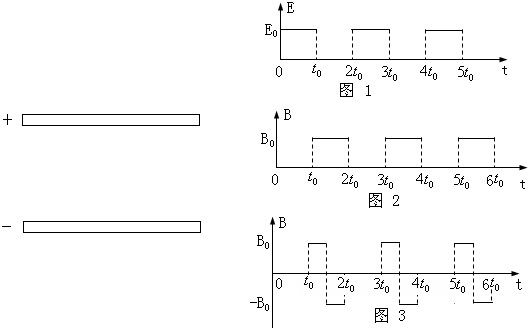
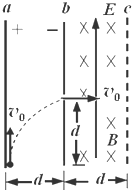 如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v0竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度
如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v0竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度