Question

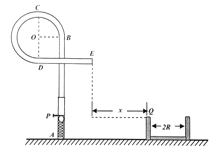
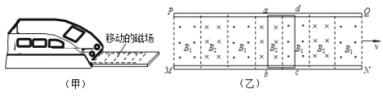
【题目】图（甲）是磁悬浮实验车与轨道示意图，图（乙）是固定在车底部金属框abcd（车厢与金属框绝缘）与轨道上运动磁场的示意图．水平地面上有两根很长的平行直导轨PQ和MN，导轨间有竖直（垂直纸面）方向等间距的匀强磁场和，二者方向相反．车底部金属框的ad边宽度与磁场间隔相等，当匀强磁场和同时以恒定速度v0沿导轨方向向右运动时，金属框会受到磁场力，带动实验车沿导轨运动．设金属框垂直导轨的ab边长L=0.20m、总电阻R=l.6Ω，实验车与线框的总质量m=2.0kg，磁场Bl=B2=1.0T，磁场运动速度．已知悬浮状态下，实验车运动时受到恒定的阻力f=0.20N，求：

（1）设t=0时刻，实验车的速度为零，求金属框受到的磁场力的大小和方向；

（2）求实验车的最大速率；

（3）实验车以最大速度做匀速运动时，为维持实验车运动，外界在单位时间内需提供的总能量？

（4）假设两磁场由静止开始向右做匀加速运动来启动实验车，当两磁场运动的时间为t=30s时，实验车正在向右做匀加速直线运动，此时实验车的速度为v=4m/s，求由两磁场开始运动到实验车开始运动所需要的时间．

Answer 1

【答案】（1）1N方向水平向右（2）8m/s（3）2J（4）

【解析】

（1）当实验车的速度为零时，线框相对于磁场的速度大小为v0，线框中左右两边都切割磁感线，产生感应电动势，则有：

所以此时金属框受到的磁场力的大小

代入数值解得

根据楞次定律可判断磁场力方向水平向右。

（2）实验车最大速率为时相对磁场的切割速率为，则此时线框所受的磁场力大小为

此时线框所受的磁场力与阻力平衡，得：

所以

（3）实验车以最大速度做匀速运动时，克服阻力的功率为

当实验车以速度匀速运动时金属框中感应电流

金属框中的热功率为

所以外界在单位时间内需提供的总能量为

（4）根据题意分析可得，为实现实验车最终沿水平方向做匀加速直线运动，其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同。

设加速度为a，则t时刻金属线圈中的电动势

金属框中感应电流

又因为安培力

所以对试验车，由牛顿第二定律得

解得

设从磁场运动到实验车起动需要时间为t0，则t0时刻金属线圈中的电动势

金属框中感应电流

又因为安培力

对实验车，由牛顿第二定律得：

即

解得由两磁场开始运动到实验车开始运动所需要的时间：

。