题目内容
（2004?广东）如图所示，ABCD是一个盆式容器，盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧，B、C为水平的，其距离d=0.50m盆边缘的高度为h=0.30m．在A处放一个质量为m的小物块并让其从静止出发下滑．已知盆内侧壁是光滑的，而盆底BC面与小物块间的动摩擦因数为μ=0.10．小物块在盆内来回滑动，最后停下来，则停的地点到B的距离为（ ）分析：根据动能定理，对小物块开始运动到停止的全过程进行研究，求出小物块在BC面上运动的总路程，再由几何关系分析最后停止的地点到B的距离．
解答：解：设小物块间在BC面上运动的总路程为S．物块在BC面上所受的滑动摩擦力大小始终为f=μmg，对小物块从开始运动到停止运动的整个过程进行研究，由动能定理得
mgh-μmgS=0
得到S=
=
m=3m，d=0.50m，则S=6d，所以小物块在BC面上来回运动共6次，最后停在B点．
故选D
mgh-μmgS=0
得到S=
| h |
| μ |
| 0.3 |
| 0.1 |
故选D
点评：本题对全过程运用动能定理进行研究，关键要抓住滑动摩擦力做功与总路程关系．
练习册系列答案
相关题目
（2004?广东）如图，画有直角坐标系Oxy的白纸位于水平桌面上，M是放在白纸上的半圆形玻璃砖，其底面的圆心在坐标的原点，直边与x轴重合，OA是画在纸上的直线，P1、P2为竖直地插在直线OA上的两枚大头针，P3是竖直地插在纸上的第三枚大头针，α是直线OA与y轴正方向的夹角，β是直线OP3与轴负方向的夹角，只要直线OA画得合适，且P3的位置取得正确，测得角α和β，便可求得玻璃得折射率．某学生在用上述方法测量玻璃的折射率，在他画出的直线OA上竖直插上了P1、P2两枚大头针，但在y＜0的区域内，不管眼睛放在何处，都无法透过玻璃砖看到P1、P2的像，他应该采取的措施是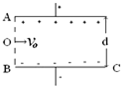
（2004?广东）如图所示，为示波管中偏转极板的示意图，相距为d、长度为l的平行板A、B加上电压后，可在A、B板之间的空间中（设为真空）产生匀强电场，在AB左端距A、B等距离处的O点，有一电荷量为q、质量为m的粒子以初速度v0沿水平方向（与AB极板平行）射入．不计重力，要使此粒子恰能从C处射出，则A、B间的电压为（ ）
（2004?广东）如图所示，密闭绝热的具有一定质量的活塞，活塞的上部封 闭着气体，下部为真空，活塞与器壁的摩擦忽略不计，置于真空中的轻弹簧的一端固定于容器的底部．另一端固定在活塞上，弹簧被压缩后用绳扎紧，此时弹簧的弹性势能为EP（弹簧处于自然长度时的弹性势能为零），现绳突然断开，弹簧推动活塞向上运动，经过多次往复运动后活塞静止，气体达到平衡态，经过此过程（ ）
（2004?广东）如图，在水平面上有两条平行导电导轨MN、PQ，导轨间距离为l，匀强磁场垂直于导轨所在的平面（纸面）向里，磁感应强度的大小为B，两根金属杆1、2摆在导轨上，与导轨垂直，它们的质量和电阻分别为m1、m2和R1、R2，两杆与导轨接触良好，与导轨间的动摩擦因数为μ，已知：杆1被外力拖动，以恒定的速度v0沿导轨运动；达到稳定状态时，杆2也以恒定速度沿导轨运动，导轨的电阻可忽略，求此时杆2克服摩擦力做功的功率．