��Ŀ����
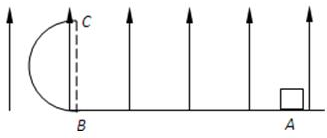
14��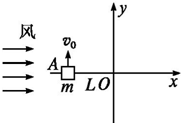 �ɻ��з��벻�����ַ綴���飮ij�η綴�����ģ����ͼ��ʾ�����㹻��Ĺ⻬ˮƽ���ϣ�����m=10kg��������������x���ϵ�Aλ�ã�-L��0���������һ����ΪL=2m�����ʲ����쳤��ϸ��˩�ӣ�ϸ�߹̶���ˮƽ��������ϵxOy��ԭ��O���ַ綴����+x��������Ҿ��Ȳ����㹻�ķ���ʹ��������ܵ��㶨ˮƽ������F=100N����t=0ʱ���ɵ���װ��ʹ���������v0=2m/s��˲ʱ�ٶȣ���������˶�ʱ����Ϊ�ʵ㣮�Լ��㣺
�ɻ��з��벻�����ַ綴���飮ij�η綴�����ģ����ͼ��ʾ�����㹻��Ĺ⻬ˮƽ���ϣ�����m=10kg��������������x���ϵ�Aλ�ã�-L��0���������һ����ΪL=2m�����ʲ����쳤��ϸ��˩�ӣ�ϸ�߹̶���ˮƽ��������ϵxOy��ԭ��O���ַ綴����+x��������Ҿ��Ȳ����㹻�ķ���ʹ��������ܵ��㶨ˮƽ������F=100N����t=0ʱ���ɵ���װ��ʹ���������v0=2m/s��˲ʱ�ٶȣ���������˶�ʱ����Ϊ�ʵ㣮�Լ��㣺��1��ϸ�߸���ֱʱ����λ������ֵ��
��2����ֱǰ��˲ʱ����������ٶȵĴ�С������x��ļнǦȣ�
��3������ٴξ���x��ʱ�ٶ�V2�ʹ�ʱ��������T��
���� ��1���������˶��ֽ�Ϊ��x���y���������ഹֱ�ķ��˶�������������ţ���˶����ɺ�λ��ʱ���ϵ������Ƿ�����λ�ƴ�С��ͨ����ϸ����ֱʱ���ǵĺ�λ�ƴ�СӦ����ϸ�ߵij��ȼ�����⣻
��2�����ݷ��˶��Ķ����Էֱ������x��y������ٶȣ�Ȼ����⼴�ɣ�
��3������ֱ˲�䣬�ɼ��ι�ϵ��֪������ֱ����нǣ�����ֱ����������������ٶ���ʧ�������ɶ��ܶ���������ٴξ���x��ʱ�ٶȣ���������֪ʶ���ʱ����������
��� �⣺��1������δ��ֱ֮ǰ�����������+x���������ٶ�Ϊ����ȼ���ֱ���˶������ٶ�Ϊax=$\frac{F}{m}$=$\frac{100}{10}$=10m/s2
��+y�������ٶ�Ϊv0������ֱ���˶���
��������������O��λ�ƴ�С�ﵽ�ߵij���Lʱ��ϸ�߽�����ֱ�����ʱ����λ������ΪB��xB��yB������
xB+L=$\frac{1}{2}$at2
yB=v0t
ϸ�߱���ֱʱ�У�L2=xB2+yB2
����5t2-2��2+��2t��2=22
��ã�t=0.8s
���ԣ�xB=1.2m��yB=1.6m
��2��vx=at=8m/s��vy=v0=2m/s
����v=2m/s
tan��=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{1}{4}$
���Ԧ�=arctan$\frac{1}{4}$
��3������ֱ˲�䣬�ɼ��ι�ϵ��֪������ֱ����нǦ�=370������ֱ����������������ٶ���ʧ������ʱ����ٶ� v1=vxcos��-vysin��=5.2m/s
�Ӵ�λ�����ٴε���x���ɶ��ܶ�����
FL��1-sin�ȣ�=$\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}$���� v2=$\sqrt{43}$m/s
����������ʽ�� T-F=m$\frac{{v}_{2}^{2}}{L}$���� T=315N
��
��1��ϸ�߸���ֱʱ����λ������ֵΪ��1.2m��1.6m����
��2����ֱǰ��˲ʱ����������ٶȵĴ�СΪ2m/s������x��ļнǦ���arctan$\frac{1}{4}$��
��3������ٴξ���x��ʱ�ٶ�v2��$\sqrt{43}$m/s����ʱ��������T��315N��
���� ���ȱ����������⣬���Բ��������ֽⷨ�����÷��˶��Ķ����Ժ͵�ʱ�ԣ�Ȼ�������Ӧ�Ĺ�����⼴�ɣ�

 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�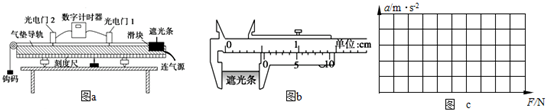
��1����ͼ�п̶ȳ߶����������������֮��ľ���x=24cm����ͼb���α꿨�߲���ڹ����Ŀ���d=0.52 cm����ʵ��С������ʵ��ʱ�����������ͼa��ʾλ���ɾ�ֹ�ͷţ������ּ�ʱ�����Զ����ڹ���ͨ�������1��ʱ���t1���ڹ���ͨ�������2��ʱ���t2���龭�������1ʱ��˲ʱ�ٶȵı���ʽv1=$\frac{d}{��{t}_{1}}$�����龭�������2ʱ��˲ʱ�ٶȵı���ʽv2=$\frac{d}{��{t}_{2}}$����ļ��ٶȵı���ʽa=$\frac{{��\frac{d}{��{t}_{2}}��}^{2}-{��\frac{d}{��{t}_{1}}��}^{2}}{2x}$��������ĸ��ʾ��
| F��N�� | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| a��m•s-2�� | 0.06 | 0.11 | 0.18 | 0.26 | 0.30 | 0.36 | 0.40 | 0.43 |
| A�� | 5OOm | B�� | 720m | C�� | 1020m | D�� | 1200m |

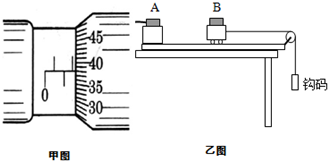 ��1����ͼ��ʾ����ͼ�����������Ķ���Ϊ1.880mm��
��1����ͼ��ʾ����ͼ�����������Ķ���Ϊ1.880mm��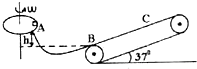 ��ͼ��ʾ��һ�뾶R=0.8m��ˮƽԲ���ƹ�Բ�ĵ���ֱ��ת����Բ�̱�Ե��һ����m=0.1kg��С���飬��Բ��ת���Ľ��ٶȴﵽijһ��ֵʱ�������Բ�̱�ԵA�㻬�䣬���⻬�Ĺ���Բ�ܣ�ͼ��Բ��δ����������⻬���AB����֪ABΪ�⻬�Ļ��ι����A����B������ˮƽ��ĸ߶�h=0.6m��������Բ�̼䶯Ħ������Ϊ��=0.5���������˶�������ʼ��δ�������������ڹ���Բ�ܴ���B��Ļ�е����ʧ���������Ϊ�ʵ㣬���Ħ���������ڻ���Ħ������g=10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ��ʾ��һ�뾶R=0.8m��ˮƽԲ���ƹ�Բ�ĵ���ֱ��ת����Բ�̱�Ե��һ����m=0.1kg��С���飬��Բ��ת���Ľ��ٶȴﵽijһ��ֵʱ�������Բ�̱�ԵA�㻬�䣬���⻬�Ĺ���Բ�ܣ�ͼ��Բ��δ����������⻬���AB����֪ABΪ�⻬�Ļ��ι����A����B������ˮƽ��ĸ߶�h=0.6m��������Բ�̼䶯Ħ������Ϊ��=0.5���������˶�������ʼ��δ�������������ڹ���Բ�ܴ���B��Ļ�е����ʧ���������Ϊ�ʵ㣬���Ħ���������ڻ���Ħ������g=10m/s2��sin37��=0.6��cos37��=0.8����
 ��ͼΪһ�綴ʵ����ģ�ͣ��綴ʵ���ҿɲ���ˮƽ����Ĵ�С�ɵ��ڵķ�����һ����Ϊ2kg������ˮƽ�����ϵ�A����12m/s�ij��ٶ�ˮƽ�����˶�������ܵ�����ķ�����С��Ϊ7N����������֮��Ķ�Ħ������Ϊ0.25������龭������ʱ�䷵��A�㣿
��ͼΪһ�綴ʵ����ģ�ͣ��綴ʵ���ҿɲ���ˮƽ����Ĵ�С�ɵ��ڵķ�����һ����Ϊ2kg������ˮƽ�����ϵ�A����12m/s�ij��ٶ�ˮƽ�����˶�������ܵ�����ķ�����С��Ϊ7N����������֮��Ķ�Ħ������Ϊ0.25������龭������ʱ�䷵��A�㣿