题目内容
6. 光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电量为q(q>0)的小球从槽的右端A处(与球心等高)无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:
光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电量为q(q>0)的小球从槽的右端A处(与球心等高)无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:(1)小球到达B点时的速度v的大小
(2)电场强度E的大小.
分析 (1)在B点,对小球进行受力分析,重力和支持力的合力提供向心力,根据向心力公式即可求解B点速度;
(2)从A到B的过程中,根据动能定理列式求出电场强度E的大小.
解答 解:(1)设小球运动到B点时速度为v,在B点,对小球进行受力分析,重力和支持力的合力提供向心力,根据向心力公式得:
N-mg=$\frac{{m{v^2}}}{R}$
由于球对轨道的压力为2mg,
所以球受到的支持力 N=2mg
解得:$v=\sqrt{gR}$
(2)从A到B根据动能定理:
mgR-qER=$\frac{1}{2}m{v^2}$
解得:$E=\frac{mg}{2q}$
答:(1)小球到达B点时的速度v的大小为$\sqrt{gR}$;
(2)电场强度E的大小为$\frac{mg}{2q}$.
点评 本题主要考查了动能定理及向心力公式的直接应用,知道电场力做功与运动路径无关,难度适中.

练习册系列答案
相关题目
14.如图,交点M的坐标为(t0,s0),在下列的说法中,正确的是( )


| A. | t0时刻,两物体在同一位置 | B. | 0~t0时间内,两物体有相同的位移 | ||
| C. | t0时刻,两物体有相等的速度 | D. | t0时刻以前P的速度总大于Q的速度 |
1.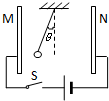 如图所示,平行板电容器的两极板M、N接于电池两极,一带电小球悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏角与竖直方向的夹角为θ,以下判断正确的是( )
如图所示,平行板电容器的两极板M、N接于电池两极,一带电小球悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏角与竖直方向的夹角为θ,以下判断正确的是( )
 如图所示,平行板电容器的两极板M、N接于电池两极,一带电小球悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏角与竖直方向的夹角为θ,以下判断正确的是( )
如图所示,平行板电容器的两极板M、N接于电池两极,一带电小球悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏角与竖直方向的夹角为θ,以下判断正确的是( )| A. | 保持S闭合,N板向M板靠近些,则θ增大 | |
| B. | 保持S闭合,N板向M板靠近些,则θ不变 | |
| C. | 断开S,N板向M板靠近些,则θ增大 | |
| D. | 断开S,N板向M板靠近些,则θ减小 |
18.下列说法正确的是( )
| A. | 富兰克林发明了避雷针 | |
| B. | 奥斯特发现了电荷之间的相互作用规律 | |
| C. | 库伦发现了电磁感应定律 | |
| D. | 麦克斯韦预言了电磁波的存在 |
15.下列叙述中正确的是( )
| A. | 匀速直线运动是速度不变的运动 | |
| B. | 匀变速直线运动是加速度不变的运动 | |
| C. | 瞬时速度可以看成是时间趋于无穷小时的平均速度 | |
| D. | 两物体相比,速度变化量较大的物体其加速度一定较大 |
16.我们在推导第一宇宙速度时,需要作一些假设.下列假设哪些是必要的( )
| A. | 卫星做匀速圆周运动 | |
| B. | 卫星的轨道半径等于地球半径 | |
| C. | 卫星的运动周期等于地球的自转周期 | |
| D. | 卫星需要的向心力等于它在地面上受到的地球引力 |
