题目内容
11.取水平地面为重力势能零点,一物块从某一高度H处水平抛出,在抛出点其动能与重力势能之比为1:3,不计空气阻力.当物块的动能与重力势能相等时,物块的速度方向与水平方向的夹角为45°,物块落地时的水平射程是$\frac{2\sqrt{3}}{3}$H.分析 根据机械能守恒定律,以及已知条件:抛出时动能恰好是重力势能的3倍,分别列式即可求出落地时速度与水平速度的关系,从而求出物块落地时的速度方向与水平方向的夹角.
解答 解:设抛出时物体的初速度为v0,当物块的动能与重力势能相等时,物块的速度为v,高度为h,与水平面之间的夹角为α.根据机械能守恒定律得:
$\frac{1}{2}m{v}_{0}^{2}$+mgH=mgh+$\frac{1}{2}$mv2=2mgh
据题有:$\frac{1}{2}m{v}_{0}^{2}$=$\frac{1}{3}$mgH
所以:${v}_{0}=\sqrt{\frac{2}{3}gH}$,h=$\frac{2}{3}H$
下落的高度:$△h=h-H=\frac{1}{3}H$
下落的时间:t=$\sqrt{\frac{2△h}{g}}$=$\sqrt{\frac{2H}{3g}}$
竖直方向的分速度:${v}_{y}=gt=\sqrt{\frac{2}{3}gH}$
物块的速度方向与水平方向的夹角满足:$tanα=\frac{{v}_{y}}{{v}_{0}}=1$
所以可得:α=45°
平抛运动的时间:t=$\sqrt{\frac{2H}{g}}$
水平射程:x=v0t=$\sqrt{\frac{2}{3}gH}×\sqrt{\frac{2H}{g}}=\frac{2\sqrt{3}}{3}H$
故答案为:45°,$\frac{2\sqrt{3}}{3}$H
点评 解决本题的关键会熟练运用机械能守恒定律处理平抛运动,并要掌握平抛运动的研究方法:运动的分解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图所示,用恒力F将质量为m的物体从地面竖直向上提升高度为h,力F对物体做功为w1,用同样的恒力F将质量为2m的物体从地面竖直向上提升高度为h,力F对物体做功为w2,则w1:w2等于( )
如图所示,用恒力F将质量为m的物体从地面竖直向上提升高度为h,力F对物体做功为w1,用同样的恒力F将质量为2m的物体从地面竖直向上提升高度为h,力F对物体做功为w2,则w1:w2等于( )
 如图所示,用恒力F将质量为m的物体从地面竖直向上提升高度为h,力F对物体做功为w1,用同样的恒力F将质量为2m的物体从地面竖直向上提升高度为h,力F对物体做功为w2,则w1:w2等于( )
如图所示,用恒力F将质量为m的物体从地面竖直向上提升高度为h,力F对物体做功为w1,用同样的恒力F将质量为2m的物体从地面竖直向上提升高度为h,力F对物体做功为w2,则w1:w2等于( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 2:1 |
19.下列说法中正确的是( )
| A. | 很小的物体就可看作质点,很大的物体一定不能看作质点 | |
| B. | 物体的运动情况不变时,选取任何物体作为参考系得到的运动规律是相同的 | |
| C. | 当研究一列火车从茂名开往北京的速度时,可把火车看作质点 | |
| D. | 当研究地球绕太阳转动时,不能把地球看作质点 |
16. 某同学去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.他先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
某同学去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.他先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
 某同学去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.他先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
某同学去实验室取定值电阻两只R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如下图,电源输出电压U=12.0V不变.他先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )| A. | U1一定大于3.0V | B. | U2一定小于9.0V | ||
| C. | U1与U2之和小于12V | D. | U1与U2之和等于12V |
20. 在t=0时甲、乙两物体同时从同一地点出发沿同一直线运动,甲做匀速运动,乙做初适度为零的匀加速运动,以出发点为参考点,它们的位移一时间(x-t)图象如图所示,设甲、乙两物体在t1时刻的速度分别为V甲、V乙,则( )
在t=0时甲、乙两物体同时从同一地点出发沿同一直线运动,甲做匀速运动,乙做初适度为零的匀加速运动,以出发点为参考点,它们的位移一时间(x-t)图象如图所示,设甲、乙两物体在t1时刻的速度分别为V甲、V乙,则( )
 在t=0时甲、乙两物体同时从同一地点出发沿同一直线运动,甲做匀速运动,乙做初适度为零的匀加速运动,以出发点为参考点,它们的位移一时间(x-t)图象如图所示,设甲、乙两物体在t1时刻的速度分别为V甲、V乙,则( )
在t=0时甲、乙两物体同时从同一地点出发沿同一直线运动,甲做匀速运动,乙做初适度为零的匀加速运动,以出发点为参考点,它们的位移一时间(x-t)图象如图所示,设甲、乙两物体在t1时刻的速度分别为V甲、V乙,则( )| A. | V甲:V乙=1:1 | |
| B. | V甲:V乙=1:2 | |
| C. | 在t1时刻甲乙两物体的相遇 | |
| D. | 在0-t1时间内甲乙两物体的平均速度相同 |
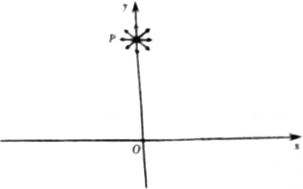 如图所示坐标系中,y轴上距原点O为d的P点有一个发射源,能够在纸面内向各个方向发射速率均为v0,质量为m,电量为q的带正电的小球,不考虑小球间的相互作用及空气阻力.
如图所示坐标系中,y轴上距原点O为d的P点有一个发射源,能够在纸面内向各个方向发射速率均为v0,质量为m,电量为q的带正电的小球,不考虑小球间的相互作用及空气阻力. 光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电量为q(q>0)的小球从槽的右端A处(与球心等高)无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:
光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电量为q(q>0)的小球从槽的右端A处(与球心等高)无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求:



 如图所示,用细绳悬挂质量为m=1kg的小球于O点,拉离竖直方向60°时放手,若L=0.5m,求小球运动到最低点N时细绳对小球的拉力多大?取g=10m/s2.
如图所示,用细绳悬挂质量为m=1kg的小球于O点,拉离竖直方向60°时放手,若L=0.5m,求小球运动到最低点N时细绳对小球的拉力多大?取g=10m/s2.