题目内容
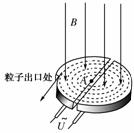
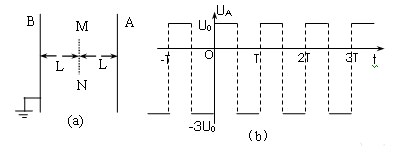
(17分)图中A和B是真空中的两块面积很大的平行金属板,加上周期为T的交流电压,在两板间产生交变的匀强电场。已知B板电势为零,A板电势UA随时间变化的规律如图(b)所示,其中UA的最大值为U0、最小值为−3U0;在图(a)中,虚线MN表示与A、B板平行等距的一个较小的面,此面到A和B的距离皆为L。在MN处,各个时刻产生机会均等的电量为q、质量为m的带负电的微粒,这种微粒产生后,在电场力的作用下从静止开始运动。设微粒一旦碰到金属板,它就附在板上不再运动,且其电量同时消失,不影响A、B板的电压。已知这种微粒的比荷恰满足![]() 。不计重力,不考虑微粒之间的相互作用。
。不计重力,不考虑微粒之间的相互作用。
(1)通过计算说明:在t =0时刻产生的微粒能否到达A板?
(2)若在t =0时刻产生的微粒能到达A板,则在t =0到t =![]() T这段时间内产生的微粒中,哪一时刻产生的粒子刚好能到达A板?
T这段时间内产生的微粒中,哪一时刻产生的粒子刚好能到达A板?
解析:
(1)由题意知,在![]() 时间内A板电势为U0,所以粒子在电场力作用
时间内A板电势为U0,所以粒子在电场力作用

(2)粒子要刚好能到达A板,就必须先做加速运动再做减速运动,到达A板的速度应为零。
设在![]() 时间内,
时间内,![]() 时刻产生的粒子能刚好到达A板。
时刻产生的粒子能刚好到达A板。
则A板电势为U0时,粒子做匀加速运动,其运动的时间为![]() ,所以这段时间的位移为:
,所以这段时间的位移为:
![]() ④ (2分)
④ (2分)
![]() 时刻的速度
时刻的速度![]() ⑤ (2分)
⑤ (2分)
之后, A板电势为-3U0,这时粒子做匀减速运动最终到达A板速度为0,设其运动的时间为![]() ,则
,则
![]() 时间内的位移
时间内的位移![]() ⑥ (1分)
⑥ (1分)
![]() 时刻的速度
时刻的速度![]() ⑦ (1分)
⑦ (1分)
由于![]() ⑧ (1分)
⑧ (1分)
![]() ⑨ (1分)
⑨ (1分)
由①④⑤⑥⑦⑧⑨得:![]()
由①④⑩解得: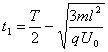 (1分)
(1分)
![]() ⑩ (1分)
⑩ (1分)

 劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的质子在加速器中被加速,且加速过程中不考虑相对论效应和重力的影响.则下列说法正确的是( )
劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的质子在加速器中被加速,且加速过程中不考虑相对论效应和重力的影响.则下列说法正确的是( )| A、质子被加速后的最大速度不可能超过2πRf | B、质子离开回旋加速器时的最大动能与加速电压U成正比 | C、质子第2次和第1次经过两D形盒间狭缝后轨道半径之比为2:1 | D、不改变磁感应强度B和交流电频率f,该回旋加速器也能用于α粒子加速 |
 劳伦斯和利文斯设计的回旋加速器工作原理如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的质子质量为m、电荷量为+q,在加速器中被加速,且加速过程中不考虑相对论效应和重力的影响.则下列说法正确的是( )
劳伦斯和利文斯设计的回旋加速器工作原理如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的质子质量为m、电荷量为+q,在加速器中被加速,且加速过程中不考虑相对论效应和重力的影响.则下列说法正确的是( )| A、质子被加速后的最大速度为2πRf | ||
| B、质子离开回旋加速器时的最大动能与加速电压U成正比 | ||
| C、质子离开回旋加速器时的最大动能与金属盒半径成正比 | ||
D、质子第1次和第2次经过D形盒间狭缝后轨道半径之比为1:
|
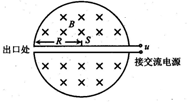 在高能物理研究中,粒子回旋加速器起着重要作用.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,磁感应强度为B的匀强磁场与盒面垂直.S处粒子源产生的粒子,质量为m、电荷量为+q,初速不计,在加速器中被加速,加速电压为玑磁场的磁感应强度为曰,D型盒的半径为R.两盒间的狭缝很小,每次加速的时间很短,可以忽略不计,加速过程中不考虑相对论效应和重力作用,下列说法正确的是( )
在高能物理研究中,粒子回旋加速器起着重要作用.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,磁感应强度为B的匀强磁场与盒面垂直.S处粒子源产生的粒子,质量为m、电荷量为+q,初速不计,在加速器中被加速,加速电压为玑磁场的磁感应强度为曰,D型盒的半径为R.两盒间的狭缝很小,每次加速的时间很短,可以忽略不计,加速过程中不考虑相对论效应和重力作用,下列说法正确的是( )A、为使正离子每经过窄缝都被加速,交变电压的频率f=
| ||
B、粒子第n次与第1次在下半盒中运动的轨道半径之比为
| ||
| C、若其它条件不变,将加速电压U增大为原来的2倍,则粒子能获得的最大动能增大为原来的2倍 | ||
| D、若其它条件不变,将D型盒的半径增大为原来的2倍,则粒子获得的最大动能增大为原来的4倍 |
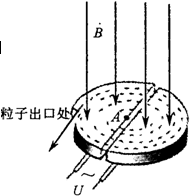 劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的质子,质量为m、电荷量为+q,在加速器中被加速,且加速过程中不考虑相对论效应和重力的影响.则
劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的质子,质量为m、电荷量为+q,在加速器中被加速,且加速过程中不考虑相对论效应和重力的影响.则