题目内容
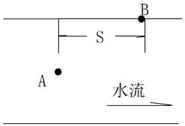 如图所示,航标灯修理工的一条小船位于200m宽的河正中A点处,从这里向下游100
如图所示,航标灯修理工的一条小船位于200m宽的河正中A点处,从这里向下游100| 3 |
分析:小船离河岸100m处,要使能安全到达河岸,则小船的合运动最大位移为
.因此由水流速度与小船的合速度,借助于平行四边形定则,即可求出小船在静水中最小速度.
1002+(100
|
解答:解:要使小船沿直线到达B点,则有合运动的最大位移为
.
因此已知小船能安全到达河岸的合速度,设此速度与水流速度的夹角为θ,
即有tanθ=
=
所以θ=30°
又已知流水速度,则可得小船在静水中最小速度为:v船=v水sinθ=
×4m/s=2m/s;
答:为了使小船沿直线到达B点,小船在静水中的速度至少2 m/.
1002+(100
|
因此已知小船能安全到达河岸的合速度,设此速度与水流速度的夹角为θ,
即有tanθ=
| 100 | ||
100
|
| ||
| 3 |
所以θ=30°
又已知流水速度,则可得小船在静水中最小速度为:v船=v水sinθ=
| 1 |
| 2 |
答:为了使小船沿直线到达B点,小船在静水中的速度至少2 m/.
点评:本题属于:一个速度要分解,已知一个分速度的大小与方向,还已知另一个分速度的大小且最小,则求这个分速度的方向与大小值.这种题型运用平行四边形定则,由几何关系来确定最小值.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 如图所示,粗细均匀的玻璃管,当温度为27℃时,封闭在管内的空气柱AB长为30cm,BC长为10cm,管内水银柱水平部分CD长为18cm,竖直部分DE长为15cm,外界大气压强为75cmHg,问:要使水平管内没有水银柱,温度至少要升高到多少℃?
如图所示,粗细均匀的玻璃管,当温度为27℃时,封闭在管内的空气柱AB长为30cm,BC长为10cm,管内水银柱水平部分CD长为18cm,竖直部分DE长为15cm,外界大气压强为75cmHg,问:要使水平管内没有水银柱,温度至少要升高到多少℃? 如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端(B与小车间的动摩擦因数为μ).某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生作用力的大小和方向为( )
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端(B与小车间的动摩擦因数为μ).某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生作用力的大小和方向为( )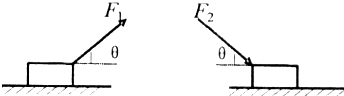
 如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,不计小球与弹簧碰撞过程中的能量损失,则小球在C点时弹簧的弹性势能为( )
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设物体在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,不计小球与弹簧碰撞过程中的能量损失,则小球在C点时弹簧的弹性势能为( )