题目内容
 如图所示,粗细均匀的玻璃管,当温度为27℃时,封闭在管内的空气柱AB长为30cm,BC长为10cm,管内水银柱水平部分CD长为18cm,竖直部分DE长为15cm,外界大气压强为75cmHg,问:要使水平管内没有水银柱,温度至少要升高到多少℃?
如图所示,粗细均匀的玻璃管,当温度为27℃时,封闭在管内的空气柱AB长为30cm,BC长为10cm,管内水银柱水平部分CD长为18cm,竖直部分DE长为15cm,外界大气压强为75cmHg,问:要使水平管内没有水银柱,温度至少要升高到多少℃?现有某同学的解法如下:
以ABC管中的气体为研究对象,各状态参量如下:p1=(75-15)cmHg=60cmHgV1=(30+10)cm?S=40cm?S(式中S为玻璃管的横截面)T1=300K.要使水平管内没有水银柱,则气体膨胀到D处,这时气体的状态参量如下:p2=(75-15-18)cmHg=42cmHgV2=(30+10+18)cm?S=58cm?S(式中S为玻璃管的横截面)T2=?
因为
| p1V1 |
| T1 |
| p2V2 |
| T2 |
所以要使水平管内没有水银柱,温度至少要升高到31.5℃
已知上述计算无误,请问该同学求得的结果是否正确?倘若有错,请求出正确结果.
分析:该同学求得的结果有错.根据气态方程
=c,温度T与pV成正比,当温度升高到T2时,水平玻璃管右端还有xcm长的水银柱,根据气态方程得到T2与x的关系式,再运用数学知识求出T2的最大值,画出T-x图象进行分析.
| pV |
| T |
解答: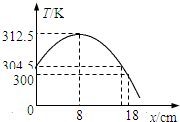 解:该同学求得的结果有错.
解:该同学求得的结果有错.
设当温度升高到T2时,水平玻璃管右端还有xcm长的水银柱,则有
p2=75-(18+15-x)=(42+x)cmHg(2分),V2=(30+28-x)S=(58-x)cm?S
由
=
,得
=
T2=-0.125x2+2x+304.5
可求得,当x=8cm时,T2有最大值312.5K(1分),即39.5℃.
画出T2随x变化的大致图象(如图所示):从图象中不难发现,当玻璃管中气体的温度逐渐升高时x从18cm起逐渐减小,当气体温度升高到304.5K时x并不为零,只要气体温度不超过312.5K(39.5℃),水平管中总有水银柱,所以要使水平管内没有水银柱,温度至少要升高到39.5℃.
答:该同学求得的结果有错,正确的结果是温度至少要升高到39.5℃.
 解:该同学求得的结果有错.
解:该同学求得的结果有错.设当温度升高到T2时,水平玻璃管右端还有xcm长的水银柱,则有
p2=75-(18+15-x)=(42+x)cmHg(2分),V2=(30+28-x)S=(58-x)cm?S
由
| p1V1 |
| T1 |
| p2V2 |
| T2 |
| 60×40 |
| 300 |
| (42+x)(58-x) |
| T2 |
T2=-0.125x2+2x+304.5
可求得,当x=8cm时,T2有最大值312.5K(1分),即39.5℃.
画出T2随x变化的大致图象(如图所示):从图象中不难发现,当玻璃管中气体的温度逐渐升高时x从18cm起逐渐减小,当气体温度升高到304.5K时x并不为零,只要气体温度不超过312.5K(39.5℃),水平管中总有水银柱,所以要使水平管内没有水银柱,温度至少要升高到39.5℃.
答:该同学求得的结果有错,正确的结果是温度至少要升高到39.5℃.
点评:本题关键要运用数学知识求T2的最大值,作出T-x图象,结合气态方程进行分析.

练习册系列答案
相关题目
 (2012?长宁区一模)如图所示,粗细均匀的U形管竖直放置,左端封闭,右端开口,左端用水银封闭着长L=10cm的理想气体,当温度为27℃时,两管水银面的高度差△h=2cm.设外界大气压为1.0×105Pa(即75cmHg).为了使左、右两管中的水银面相平,求:
(2012?长宁区一模)如图所示,粗细均匀的U形管竖直放置,左端封闭,右端开口,左端用水银封闭着长L=10cm的理想气体,当温度为27℃时,两管水银面的高度差△h=2cm.设外界大气压为1.0×105Pa(即75cmHg).为了使左、右两管中的水银面相平,求: (2011?上海二模)如图所示,粗细均匀的U形管,左端封闭,右端开口,左端用水银封闭着长L=15cm的理想气体,当温度为27℃时,两管水银面的高度差△h=3cm.设外界大气压为1.0×105Pa(即75cmHg).则:
(2011?上海二模)如图所示,粗细均匀的U形管,左端封闭,右端开口,左端用水银封闭着长L=15cm的理想气体,当温度为27℃时,两管水银面的高度差△h=3cm.设外界大气压为1.0×105Pa(即75cmHg).则: [物理--选修3-3]
[物理--选修3-3]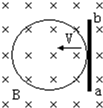 如图所示.粗细均匀的电阻为r的金属圆环放在磁感应强度为B的垂直环面的匀强磁场中,圆环的直径为d.长为d、电阻为
如图所示.粗细均匀的电阻为r的金属圆环放在磁感应强度为B的垂直环面的匀强磁场中,圆环的直径为d.长为d、电阻为