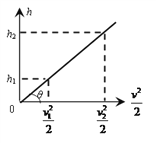
��Ŀ����
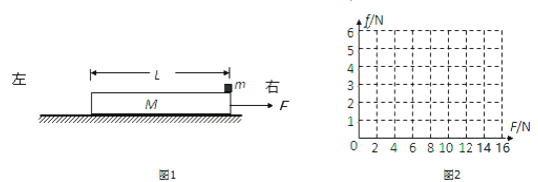
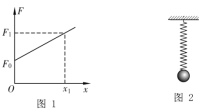
����Ŀ��ijͬѧ��ʵ�������ҵ�һ���������ɣ������������䵯��F�뵯���쳤��x�Ĺ�ϵ��ͼ1��ʾ��ͼ��F0��F1��x1��֪�����ֽ���������϶˹̶����¶˽�һ����Ϊm��С��С��ֹ��С��������һС�ξ��루�ڵ��ɵĵ������ڣ�����ʱ���ɵ��쳤��Ϊx2��Ȼ���ɾ�ֹ�ͷ�С��С������ֱ���������������ɺ��Բ��ƣ��������ٶ�Ϊg����С���ٶȴﵽ���ʱ���ɵ��쳤��Ϊ
A��![]() B��
B��![]() C��
C��![]() D��
D��![]()
���𰸡�C
��������
�����������������������һ������ĵ��ɣ���Ȼ״̬�£����ɵĸ�Ȧ�ǽ��ܰ���һ��ģ�������Ǽ�ѹ�ģ�����ý����ɵ�һ�˹̶�����һ����һ��������������������ɣ����ɲ��������Ͼ��쳤������Ҫ����ijһֵʱ�Żᷢ���α䣬Ҳ�������е�F0�����������������ɵij�ʼ������ʵ����F0��һ���ٽ�״̬����������ΪF0ʱ��������Ϊ����û���쳤����ʱ���ɸ�Ȧ�仹�Ӵ������Ѿ�û�м�ѹ�����ˡ����������ĵ�������Ҫע�⣬F=kx��kΪ����ϵ����xΪ�α������Ѿ��������ˣ������������ɵĵ����ɱ�ʾΪF=F0+kx��F0Ϊ��ʼ������kΪ����ϵ����xΪ�α������������е�ͼ1��֪��![]() ��
��
��С������ֱ������ʱ�����ɵĵ���![]() ʱС����ٶ�������ʱ���ɵ��α���Ϊ
ʱС����ٶ�������ʱ���ɵ��α���Ϊ![]() ������
������![]() ����������k�ı���ʽ������ɵ�
����������k�ı���ʽ������ɵ�![]() ����C��ȷ
����C��ȷ