题目内容
10.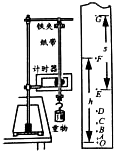 用如图所示的装置来探究自由落体运动过程中动能与势能的转化和守恒,某同学按图示安装仪器,并打出来一条纸带,图中O点是打出的第一个点迹,A、B、C、D、E、F、G是依次打出的点,量出OF间的距离为h,EG之间的距离为s.已知打点计时器的周期为T,重物的质量为m,当地的重力加速度为g.则打F点时重物速度的大小为$\frac{s}{2T}$,从打O点到打F点过程中,重物重力势能的减少量为mgh、重物动能的增加量为$\frac{m{s}^{2}}{8{T}^{2}}$.
用如图所示的装置来探究自由落体运动过程中动能与势能的转化和守恒,某同学按图示安装仪器,并打出来一条纸带,图中O点是打出的第一个点迹,A、B、C、D、E、F、G是依次打出的点,量出OF间的距离为h,EG之间的距离为s.已知打点计时器的周期为T,重物的质量为m,当地的重力加速度为g.则打F点时重物速度的大小为$\frac{s}{2T}$,从打O点到打F点过程中,重物重力势能的减少量为mgh、重物动能的增加量为$\frac{m{s}^{2}}{8{T}^{2}}$.
分析 纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,进一步求出物体的动能变化,根据下落高度计算重力势能的变化.
解答 解:从打O点到打F点过程中,据重力势能的定义式得重力势能减小量为:△Ep=mgh
利用匀变速直线运动的推论得F点的速度为:vF=$\frac{{x}_{EG}}{{t}_{EG}}$=$\frac{\frac{s}{2}}{T}$=$\frac{s}{2T}$
动能的变化量大小为:△Ek=$\frac{1}{2}$m${v}_{F}^{2}$-0=$\frac{m{s}^{2}}{8{T}^{2}}$
故答案为:$\frac{s}{2T}$,mgh,$\frac{m{s}^{2}}{8{T}^{2}}$.
点评 带问题的处理是力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度;要知道重物带动纸带下落过程中能量转化的过程和能量守恒.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
4.甲、乙两人在一幢楼的三层窗口比赛掷垒球,他们都尽力沿水平方向掷出同样的垒球,不计空气阻力.甲掷的水平距离正好是乙的两倍.若乙要想水平掷出相当于甲在三层窗口掷出的距离,则乙应( )
| A. | 在6层窗口水平掷出 | B. | 在9层窗口水平掷出 | ||
| C. | 在12层窗口水平掷出 | D. | 在16层窗口水平掷出 |
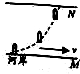
 竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向夹角为30°,如图所示,则可知玻璃管水平方向的移动速度为1.73m/s,若玻璃管的长度为0.1m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平的距离为1.73m.
竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向夹角为30°,如图所示,则可知玻璃管水平方向的移动速度为1.73m/s,若玻璃管的长度为0.1m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平的距离为1.73m.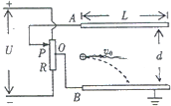 如图所示,水平放置的平行板电容器的极板长L=0.4m,两板间距离d也为0.4m,A极板通过滑动触头P与电阻R相接触,B极板与电阻R的中点O点固定连接且接地.电阻R两端与一恒定电压的电源相连,其正负极性如图所示.
如图所示,水平放置的平行板电容器的极板长L=0.4m,两板间距离d也为0.4m,A极板通过滑动触头P与电阻R相接触,B极板与电阻R的中点O点固定连接且接地.电阻R两端与一恒定电压的电源相连,其正负极性如图所示.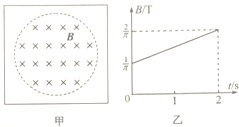 如图甲所示,一边长L=0.5m的长方形单匝金属线圈,处在一半径r=0.2m的圆形均匀磁场中,其磁场感应强度B随时间变化规律如图乙所示,线圈平面垂直磁场,金属线圈的电阻R=1Ω.求:
如图甲所示,一边长L=0.5m的长方形单匝金属线圈,处在一半径r=0.2m的圆形均匀磁场中,其磁场感应强度B随时间变化规律如图乙所示,线圈平面垂直磁场,金属线圈的电阻R=1Ω.求: 如图所示,小船在静水中匀速运动,当它在流速v恒定的河水中,船头向着与河岸垂直方向航行时,下图中航线正确的是( )
如图所示,小船在静水中匀速运动,当它在流速v恒定的河水中,船头向着与河岸垂直方向航行时,下图中航线正确的是( )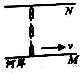


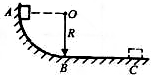 如图所示,光滑$\frac{1}{4}$圆弧AB的半径R=0.8m,有一质量为m=1.0kg的物体自A点由静止开始沿弧面下滑,到B点后又沿水平面滑行,最后停止在水平面上的C点.已知物体与水平面之间的动摩擦因数μ=0.4,取g=10m/s2,求:
如图所示,光滑$\frac{1}{4}$圆弧AB的半径R=0.8m,有一质量为m=1.0kg的物体自A点由静止开始沿弧面下滑,到B点后又沿水平面滑行,最后停止在水平面上的C点.已知物体与水平面之间的动摩擦因数μ=0.4,取g=10m/s2,求: