题目内容
20.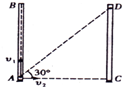 竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向夹角为30°,如图所示,则可知玻璃管水平方向的移动速度为1.73m/s,若玻璃管的长度为0.1m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平的距离为1.73m.
竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.1m/s速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动方向与水平方向夹角为30°,如图所示,则可知玻璃管水平方向的移动速度为1.73m/s,若玻璃管的长度为0.1m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平的距离为1.73m.
分析 红蜡块的水平分运动和竖直分运动均是匀速直线运动,已知竖直分速度,根据平行四边形定则判断玻璃管水平运动的速度.
解答 解:红蜡块的水平分运动和竖直分运动均是匀速直线运动,根据平行四边形定则作图,如下: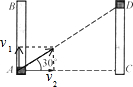
故v2=$\frac{{v}_{1}}{tan30°}$=$\frac{0.1}{\frac{\sqrt{3}}{3}}$≈1.73m/s;
因玻璃管的长度为0.1m,则玻璃管水平的距离为s=0.1$\sqrt{3}$m=1.73m;
故答案为:1.73,1.73.
点评 解决本题的关键知道运动的合成和分解遵循平行四边形定则,注意三角函数的正确运用,及关注夹角.

练习册系列答案
相关题目
11. 如图为某电场中的一条电场线,a、b、c为电场线上的三点,其中c为a、b的中点.若一负电荷仅在电场力作用下运动先后经过a、b点,做加速度增大的加速运动,Ep电势能,E为电场强度,φ为电势,U为电势差,则( )
如图为某电场中的一条电场线,a、b、c为电场线上的三点,其中c为a、b的中点.若一负电荷仅在电场力作用下运动先后经过a、b点,做加速度增大的加速运动,Ep电势能,E为电场强度,φ为电势,U为电势差,则( )
 如图为某电场中的一条电场线,a、b、c为电场线上的三点,其中c为a、b的中点.若一负电荷仅在电场力作用下运动先后经过a、b点,做加速度增大的加速运动,Ep电势能,E为电场强度,φ为电势,U为电势差,则( )
如图为某电场中的一条电场线,a、b、c为电场线上的三点,其中c为a、b的中点.若一负电荷仅在电场力作用下运动先后经过a、b点,做加速度增大的加速运动,Ep电势能,E为电场强度,φ为电势,U为电势差,则( )| A. | Epa>Epc>Epb | B. | Ea>Ec>Eb | C. | φa<φc<φb | D. | Uca<Ubc |
15.对于质量为m1和m2(m1>m2)的两个物体间的万有引力的表达式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | m1受到的引力大于m2受到的引力 | |
| B. | 两个物体间的引力总是大小相等、方向相反,是一对平衡力 | |
| C. | 当两个物体间的距离r趋于零时,万有引力趋于无穷大 | |
| D. | 公式中的G是引力常量,它是由英国物理学家卡文迪许在实验室测量得出的 |
5.下列关于功和能的说法正确的是( )
| A. | 功就是能,能就是功 | |
| B. | 滑动摩擦力只能做负功 | |
| C. | 由于自然界遵循能量守恒定律,从长远来看,能源危机是不存在的 | |
| D. | 能量转化的多少可以用功来量度 |
12.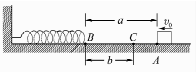 如图,质量为m的物体(可视为质点)沿水平面向左运动,经过A点时速度为v0,滑过AB段后在B点与轻弹簧接触并发生相互作用,作用前弹簧处于原长,弹簧先被压缩,而后又将物体弹回,物体向右滑到C处恰好静止.已知AB=a,BC=b,且物体只与水平面AB间有摩擦,动摩擦因数为μ,取重力加速度为g.则( )
如图,质量为m的物体(可视为质点)沿水平面向左运动,经过A点时速度为v0,滑过AB段后在B点与轻弹簧接触并发生相互作用,作用前弹簧处于原长,弹簧先被压缩,而后又将物体弹回,物体向右滑到C处恰好静止.已知AB=a,BC=b,且物体只与水平面AB间有摩擦,动摩擦因数为μ,取重力加速度为g.则( )
 如图,质量为m的物体(可视为质点)沿水平面向左运动,经过A点时速度为v0,滑过AB段后在B点与轻弹簧接触并发生相互作用,作用前弹簧处于原长,弹簧先被压缩,而后又将物体弹回,物体向右滑到C处恰好静止.已知AB=a,BC=b,且物体只与水平面AB间有摩擦,动摩擦因数为μ,取重力加速度为g.则( )
如图,质量为m的物体(可视为质点)沿水平面向左运动,经过A点时速度为v0,滑过AB段后在B点与轻弹簧接触并发生相互作用,作用前弹簧处于原长,弹簧先被压缩,而后又将物体弹回,物体向右滑到C处恰好静止.已知AB=a,BC=b,且物体只与水平面AB间有摩擦,动摩擦因数为μ,取重力加速度为g.则( )| A. | 整个过程中,摩擦力产生的热量为$\frac{1}{2}$mv02 | |
| B. | 整个过程中,摩擦产生的热量为μmg(a-b) | |
| C. | 弹簧的最大弹性势能为$\frac{1}{2}$mv02-μmga | |
| D. | 弹簧的最大弹性势能为μmgb |
9.关于电场线和磁感应线的说法正确的是( )
| A. | 电场线是点电荷在电场中的运动轨迹 | |
| B. | 磁感线是磁场中铁屑排列成的曲线 | |
| C. | 电场线和磁感线都是假想曲线 | |
| D. | 磁感线从N极出发至S极终止 |
 用如图所示的装置来探究自由落体运动过程中动能与势能的转化和守恒,某同学按图示安装仪器,并打出来一条纸带,图中O点是打出的第一个点迹,A、B、C、D、E、F、G是依次打出的点,量出OF间的距离为h,EG之间的距离为s.已知打点计时器的周期为T,重物的质量为m,当地的重力加速度为g.则打F点时重物速度的大小为$\frac{s}{2T}$,从打O点到打F点过程中,重物重力势能的减少量为mgh、重物动能的增加量为$\frac{m{s}^{2}}{8{T}^{2}}$.
用如图所示的装置来探究自由落体运动过程中动能与势能的转化和守恒,某同学按图示安装仪器,并打出来一条纸带,图中O点是打出的第一个点迹,A、B、C、D、E、F、G是依次打出的点,量出OF间的距离为h,EG之间的距离为s.已知打点计时器的周期为T,重物的质量为m,当地的重力加速度为g.则打F点时重物速度的大小为$\frac{s}{2T}$,从打O点到打F点过程中,重物重力势能的减少量为mgh、重物动能的增加量为$\frac{m{s}^{2}}{8{T}^{2}}$.