题目内容
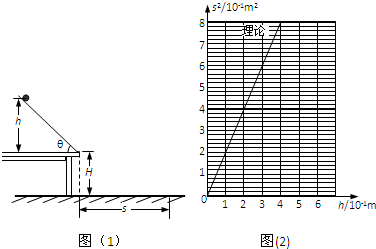
如图(1)所示,某同学采用双线摆和光电计数器测量重力加速度.设每根悬线长l,两悬点间相距s,金属小球半径为r,AB为光电计数器.现将小球垂直于纸面向外拉动,使悬线偏离竖直方向一个较小的角度并由静止释放,同时启动光电计数器,当小球第一次经过图中虚线(光束)位置O时,由A射向B的光束被挡住,计数器计数一次,显示为“1”,同时由零开始计时,而后每当小球经过O点时,计数器都要计数一次.当计数器上显示的计数次数刚好为n时,计时时间为t.
(1)计算重力加速度g时,双线摆的等效摆长L为 ;最后依据公式g= ,代入周期T和等效摆长L的值即可求出重力加速度.(用题中字母表示)
(2)使用20分度游标卡尺测出摆球直径如图(2)所示,则测得摆球的半径r= ×10-3m.
(3)当计数器上显示的计数次数刚好为“85”时,按停秒表.秒表示数如图(3)所示.则测得双线摆的周期T=
s.(结果保留三位有效数字)

(1)计算重力加速度g时,双线摆的等效摆长L为
(2)使用20分度游标卡尺测出摆球直径如图(2)所示,则测得摆球的半径r=
(3)当计数器上显示的计数次数刚好为“85”时,按停秒表.秒表示数如图(3)所示.则测得双线摆的周期T=
分析:(1)双线摆的等效摆长等于球心到悬挂处得垂直距离.根据T=2π
,所以实验的原理是g=
.
(2)游标卡尺的读数等于主尺读数加游标读数.
(3)秒表的读数等于小盘读数和大盘读数之和.完成一次全振动的时间为一个周期,所以周期等于所测时间除以全振动的次数.
|
| 4π2L |
| T2 |
(2)游标卡尺的读数等于主尺读数加游标读数.
(3)秒表的读数等于小盘读数和大盘读数之和.完成一次全振动的时间为一个周期,所以周期等于所测时间除以全振动的次数.
解答:解:(1)双线摆的等效摆长L=r+
=
+ r.根据T=2π
,所以最后依据公式g=
.
(2)游标卡尺的主尺读数22mm,游标读数为0.05×4=0.20mm.所以最终读数为22.20mm.所以半径为
=11.10mm=11.10×10-3m.
(3)秒表的读数为60+11.3s=71.3s.T=
s=1.70s.
故本题答案为:(1)
+ r,
(2)11.10 (3)1.70
l2-(
|
l2-
|
|
| 4π2L |
| T2 |
(2)游标卡尺的主尺读数22mm,游标读数为0.05×4=0.20mm.所以最终读数为22.20mm.所以半径为
| 22.20mm |
| 2 |
(3)秒表的读数为60+11.3s=71.3s.T=
| 71.3 |
| 42 |
故本题答案为:(1)
l2-
|
| 4π2L |
| T2 |
点评:解决本题的关键掌握单摆的周期公式T=2π
,以及知道如何去测周期.
|

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
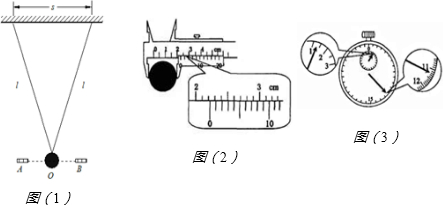
某同学利用如图(1)所示的实验装置验证机械能守恒定律.倾角θ=37°的轨道末端有一段很短的光滑小圆弧,可使钢球从离地H的高度处水平飞出.将钢球从轨道的不同高度h静止释放,测出相应的钢球落点距轨道末端的水平距离s:
(1)若轨道完全光滑,s2与h的理论关系应满足s2=______(用H、h表示),该同学根据理论值在图(2)中做出了s2-h关系图象.
(2)该同学经实验测量得到一组数据,如下表所示:请在图(2)的坐标纸上做出实验所得的s2-h关系图.
(3)对比实验结果与理论计算得到的s2-h图象,自同一高度释放的钢球,水平抛出的实际速率______(填“大于”或“小于”)理论值.
(4)该同学通过分析确定是因为轨道的粗糙造成了实验得到的图象与理论图象有较大的差异,请根据两个图象算出倾斜轨道与钢球间的动摩擦因素μ=______.

(1)若轨道完全光滑,s2与h的理论关系应满足s2=______(用H、h表示),该同学根据理论值在图(2)中做出了s2-h关系图象.
(2)该同学经实验测量得到一组数据,如下表所示:请在图(2)的坐标纸上做出实验所得的s2-h关系图.
| h(10-1m) | 2.00 | 3.00 | 4.00 | 5.00. | 6.00 |
| s2(10-1m2) | 2.60 | 3.90 | 5.20 | 6.50 | 7.80 |
(4)该同学通过分析确定是因为轨道的粗糙造成了实验得到的图象与理论图象有较大的差异,请根据两个图象算出倾斜轨道与钢球间的动摩擦因素μ=______.
 某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即
某研究性学习小组用如图(a)所示装置验证机械能守恒定律.让一个摆球由静止开始从A位置摆到B位置,若不考虑空气阻力,小球的机械能应该守恒,即