Question

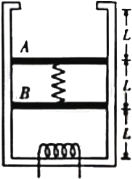
【题目】总质量为M的两物块A、B静止叠放在水平面上，用轻绳通过滑轮将A、B连接，A与B及水平面间的动摩擦因数均为μ，对滑轮轴施加一个水平力F，如图所示．（忽略滑轮质量，不计其它阻力， g＝10 m/s2.）

（1）若A、B能以相同的加速度向右运动，求加速度表达式？

（2）若A、B能以相同的加速度向右运动，求B物块的质量m与总质量之间应该满足的条件？

（2）若mA＝4 kg、mB＝2 kg，μ＝0.5，要使A能在水平面上运动，求水平力F应满足的条件？

Answer 1

【答案】(1) (2)m≥M　(3)F>40N

【解析】

(1)设物块B的质量为m，A、B的加速度为a，A、B间的摩擦力为f，对整体由牛顿第二定律得

F－μMg＝Ma

解得：

(2)对物块B，有

－f＝ma

f≤μmg

联立解得

则有

(3)依题意可知mA>mB，A、B有不同的加速度，设加速度分别为a1、a2，并假定此时B受到的滑动摩擦力向左，A、B受力如图，由牛顿第二定律可得

－μ(mA＋mB)g＋μmBg＝mAa1

解得

F＝2mA(μg＋a1)

其中a1>0，因此

F>40N

对B物体：

－μmBg＝mBa2

F＝40N时B的加速度

a2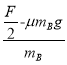＝ ＝5m/s2>a1

假定成立，即水平力F必须大于40N，物块A才能在水平面上运动