��Ŀ����
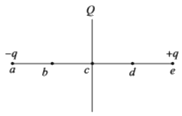
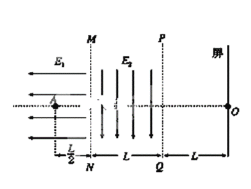
����Ŀ����ͼ��ʾ������MN�����һ��ǿΪE1=E����ǿ�糡��������ƽ�е�����MN��PQ֮������ſ�ΪL���糡ǿ��ΪE2=2E����ǿ�糡��������PQ�Ҳ����ΪL����һ��糡E2ƽ�е������ֽ�һ���ӣ������Ϊe������Ϊm�����ٶȵط���糡E1�е�A�㣬�����Ӵ����Ҳ�����ϣ�AO����������ֱ������ΪO����
��1�����Ӵ��ͷŵ����������õ�ʱ�䣻
��2�����Ӹ�����糡E2ʱ���ٶȷ�����AO���н���������ֵtan����
��3�����Ӵ����ϵĵ�P������O�ľ���x
���𰸡���1��![]() ���� 2��tan��=2�� ��3��3L��
���� 2��tan��=2�� ��3��3L��
��������
��1�������ڵ糡E1�������ٶ�Ϊ����ȼ���ֱ���˶�������ٶ�Ϊa1��ʱ��Ϊt1��
��ţ�ٵڶ����ɵã�
![]() ��
��
��![]() �ã�
�ã�
![]() ��
��
���ӽ���糡E2ʱ���ٶ�Ϊ��
v1=a1t1 ��
����糡E2����ˮƽ����������ֱ���˶���ʱ��Ϊ��
![]() ��
��
���Ӵ��ͷŵ����������õ�ʱ��Ϊ��
t=t1+t2 ��
�������������ã�
![]() ��
��
��2������������糡E2ʱƽ�е糡������ٶ�Ϊvy
��ţ�ٵڶ����ɵã����ӽ���糡E2ʱ�ļ��ٶ�Ϊ��
![]() ��
��
vy=a2t3 ��
![]() ��
��
���Ӹ�����糡E2ʱ���ٶȷ�����AO���нǵ�����ֵΪ��
![]() ��
��
�����٢ڢۢޢߢ��ã�
tan��=2 ��
��3�����������ڵ糡�е��˶��켣��ͼ��ʾ��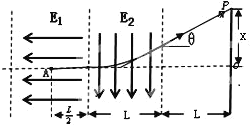
����Ӵ����ϵĵ�P��O��ľ���x��������ͼ�м��ι�ϵ�ã�
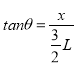 ��11��
��11��
�����⣨11���ã�
x=3L