Question

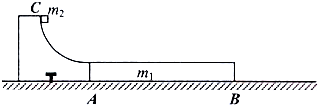
如图所示，质量m₁=2.0kg的木板AB静止在水平面上，木板的左侧有一个固定的半径R=0.60m的四分之一圆弧形轨道，轨道末端的切线水平，轨道与木板靠在一起，且末端高度与木板高度相同．现将质量m₂=1.0kg可视为质点的小木块C，从圆弧形轨道顶端由静止释放，小木块C到达圆弧形轨道底端时的速度v₀=3.0m/s．之后小木块C滑上木板AB并带动木板AB运动，当小木块C离开木板AB右端B时，木板AB的速度v₁=0.5
m/s，在小木块C在木板AB上滑行的过程中，小木块C与木板AB总共损失的动能△E=2.25J．小木块C与木板AB间的动摩擦因数μ=0.1．木板AB与地面间的摩擦及空气阻力可忽略不计．取g=10m/s²．求
（1）小木块C运动到圆弧形轨道末端时所受支持力的大小；
（2）小木块C在圆弧形轨道上下滑过程中克服摩擦力所做的功；
（3）小木块C在木板AB上运动过程中，小木块C相对于地面的位移．

Answer 1

（1）小木块通过圆弧形轨道末端时，
由牛顿第二定律得：F-m₂g=

m2 v 20

R

，
解得小木块受到的支持力：F=25N；
（2）小木块在圆弧形轨道上下滑过程中，
由动能定理得：m₂gR-W_f=

1

2

m₂v₀²-0，
解得克服摩擦力做的功W_f=1.5J；
（3）木块C与木板AB间的摩擦力f=μm₂g，
由动能定理得：
对木板：fs₁=

1

2

m₁v₁²-0，
对小木块：-fs₂=

1

2

m₂（v₂²-v₀²），
木块与木板间的位移关系：s₂=s₁+L，
小木块与木板总共损失的动能△E=fL，
解得：s₂=2.5m；
答：（1）小木块C运动到圆弧形轨道末端时所受支持力大小为25N；
（2）小木块C在圆弧形轨道上下滑过程中克服摩擦力所做的功为1.5J；
（3）小木块C在木板AB上运动过程中，小木块C相对于地面的位移为2.5m．