题目内容
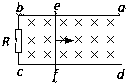如图所示，在一匀强磁场中有一足够长的U形导线框abcd，线框处于水平面内，磁场与线框平面垂直，R为一电阻，ef为垂直于ab的一根导体杆，它可以在ab、cd上无摩擦地滑动．杆ef及线框中导线的电阻都可不计．开始时，给ef一个向右的初速度，则（ ）| A、ef将向右匀减速运动 | B、ef运动的加速度越来越小 | C、R的热功率均匀减小 | D、ef减少的动能等于R产生的热量 |
分析：金属棒向右运动时会切割磁感线产生感应电动势和感应电流，金属杆ef受到向左的安培力做减速运动，速度减小会造成感应电动势和感应电流减小，安培力也随之减小，所以物体做减速运动的加速度会减小，直到速度为零时金属杆静止．先分析棒的运动情况，再根据能量守恒分析ef动能的减少量与R产生的热量关系．
解答：解：A、B金属棒向右运动时会切割磁感线产生感应电动势和感应电流，根据右手定则判断可知，ef中感应电流方向从f到e．
根据左手定则判断可知，ef所受的安培力向左，则ef将向右做减速运动．
感应电流表达式为：I=
=
金属棒所受的安培力大小表达式为：F=BIL=
，可知随着速度的减小，安培力减小．所以ef做加速度减小的变减速运动，最终停止运动，故A错误，B正确．
C、由于棒做加速度减小的变减速运动，速度不是均匀减小，由I=
知感应电流不是均匀减小，R的热功率为 P=I2R，可知R的热功率也不是均匀减小．故C错误．
D、根据能量守恒可知：ef减少的动能全部转化为R产生的内能，则ef减少的动能等于R产生的热量，故D正确，
故选：BD
根据左手定则判断可知，ef所受的安培力向左，则ef将向右做减速运动．
感应电流表达式为：I=
| E |
| R |
| BLv |
| R |
金属棒所受的安培力大小表达式为：F=BIL=
| B2L2v |
| R |
C、由于棒做加速度减小的变减速运动，速度不是均匀减小，由I=
| BLv |
| R |
D、根据能量守恒可知：ef减少的动能全部转化为R产生的内能，则ef减少的动能等于R产生的热量，故D正确，
故选：BD
点评：此类题目的解题关键点是能够灵活应用法拉第电磁感应定律与右手定则、左手定则，推导出安培力的表达式判断其变化．
练习册系列答案
相关题目
如图所示，在与匀强磁场垂直的平面内放置一个折成锐角的导线框MON，∠MON=α．在它上面搁置另一根与ON垂直的直导线PQ，PQ紧贴OM、ON，并以平行于ON的速度v从顶角O开始向右匀速滑动．设线框MON和直导线PQ单位长度的电阻为R0，磁感强度为B，则回路中的感应电流的方向为
（1）如图所示，在一匀强电场中，将q=-2×10-6C的负电荷由A点移至B点，需克服电场力做功W=4×10-5J，已知AB连线长为0.1m，AB连线与电场线间的夹角θ=60°，则A、B两点间的电势差
