题目内容
【题目】如图所示,半径为R1=1.8m的四分之一光滑圆弧轨道与半径为R2=0.5m的半圆光滑细圆管轨道平滑连接并固定在竖直平面内,光滑水平地面上紧靠管口有一长度为L=2.0m、质量为M=1.5kg的木板,木板上表面正好与管口底部相切,处在同一水平线上,木板的左方有一足够长的台阶,其高度正好与木板相同。现在让质量为m1=2kg的小物块A从四分之一圆弧顶部由静止释放,然后与静止于该圆弧底部质量为m2=1kg的小物块B发生碰撞,二者形成一个整体C不再分开,之后从半圆管轨道底部滑上木板,木板由静止开始向左运动.当木板速度为v=2m/s时,与台阶碰撞立即被粘住(即速度变为零).若重力加速度g取10m/s2,小物块碰撞前后均可视为质点,圆管粗细不计.
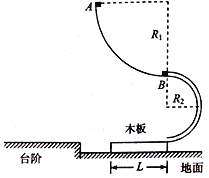
(1)求物块A和B碰撞过程中损失的机械能。
(2)求物块C滑到半圆管底部时所受支持力大小.
(3)若物块与木板及台阶表面间的动摩擦因数均为μ=0.25,求物块C在台阶表面上能滑行的距离。
【答案】(1)12J (2)246N (3)4.8m
【解析】试题分析:(1)由机械能守恒定律可以求出A的速度,碰撞过程系统动量守恒,应用动量守恒定律与能量守恒定律可以求出损失的机械能。(2)应用动能定理求出物块到达C点时的速度,然后应用牛顿第二定律求出支持力。(3)应用动量守恒定律与动能定理求出物块在台阶上滑行的最大距离。
(1)设小物块A滑到底部时的速度为![]() ,由机械能守恒得:
,由机械能守恒得:![]()
A、B碰撞满足动量守恒定律,则有:![]()
设碰撞过程中损失的机械能为![]() ,则
,则![]()
解得:![]()
(2)设小物块C在半圆管底部的速度为![]() ,由机械能守恒定律得:
,由机械能守恒定律得:![]()
物块C在半圆管底部时由牛顿第二运动定律得:![]()
解得:![]()
(3)设物块C滑上木板后,当木板速度为![]() 时其速度为
时其速度为![]()
由动量守恒定律得:![]()
设物块C从滑上木板直到木板被粘住,相对木板运动的位移为![]()
由能量守恒定律得:![]()
此时物块C到木板左端的距离为![]()
设物块C能在台阶上运动的距离为![]() ,由动能定理得:
,由动能定理得:![]()
联立以上方程可解得![]()

 天天练口算系列答案
天天练口算系列答案【题目】某同学用如图甲所示的实验电路做“测定电源的电动势和内阻”实验,现备有以下器材:
A.干电池1节
B.滑动变阻器(0~50 Ω)
C.电压表(0~3 V)
D.电压表(0~15 V)
E.电流表(0~0.6 A)
F.电流表(0~3 A)
(1)其中电压表应选________,电流表应选________;(填字母)
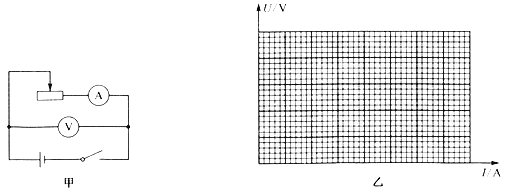
(2)该同学测量时记录了5组数据,并将数据填入以下表格中.请你根据这些数据在图乙坐标系中画出U-I图线,根据图线求出电池的电动势E=________V,内阻r=________Ω;
次数 | 1 | 2 | 3 | 4 | 5 |
I/A | 0.15 | 0.25 | 0.36 | 0.45 | 0.56 |
U/V | 1.40 | 1.35 | 1.30 | 1.25 | 1.20 |
(3)该同学对以上实验的系统误差和导致的结果进行了分析,其中正确的是______.(填字母)
A.主要是由电流表的分压引起的
B.主要是由电压表的分流引起的
C.内阻测量值大于真实值
D.电动势测量值小于真实值