题目内容
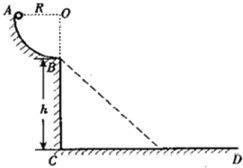
如图所示,半径为R=0.4m的半圆形光滑轨道固定在水平地面上,A与B两点在同一竖直线上,质量为m=0.5kg的小球以某一初速度自A点进入半圆形轨道,沿轨道上升到最高点B后,以一定的速度水平飞出,最后落在水平地面上的C点,现测出AC=1.2m.(co53°=0.6,sin53°=0.8)求:
(1)小球飞出B时的速度
(2)小球飞出前对B的作用力
(3)小球落在水平地面上C点时的速度.

(1)小球飞出B时的速度
(2)小球飞出前对B的作用力
(3)小球落在水平地面上C点时的速度.

(1)根据2R=
gt2得,t=
=
s=0.4s,
则小球飞出B点的速度vB=
=
=3m/s.
(2)根据牛顿第二定律得,mg+N=m
解得N=m
-mg=0.5×
-5N=6.25N.
(3)小球到达C点时竖直分速度vy=gt=4m/s,
则vC=
=
=5m/s.
答:(1)小球飞出B点的速度为3m/s;
(2)小球飞出前对B的作用力为6.25N;
(3)小球落在水平面上C点的速度为5m/s.
| 1 |
| 2 |
|
|
则小球飞出B点的速度vB=
| x |
| t |
| 1.2 |
| 0.4 |
(2)根据牛顿第二定律得,mg+N=m
| vB2 |
| R |
解得N=m
| vB2 |
| R |
| 9 |
| 0.4 |
(3)小球到达C点时竖直分速度vy=gt=4m/s,
则vC=
| vy2+vB2 |
| 9+16 |
答:(1)小球飞出B点的速度为3m/s;
(2)小球飞出前对B的作用力为6.25N;
(3)小球落在水平面上C点的速度为5m/s.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
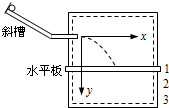
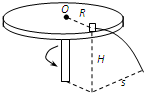
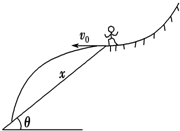
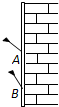
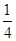 圆弧),则由此可知物体是做( ).
圆弧),则由此可知物体是做( ).