题目内容
如图所示,用细绳一端系着的质量为M=0.6kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为m=0.3kg的小球B,A的重心到O点的距离为0.2m.若A与转盘间的最大静摩擦力为f=2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(取g=10m/s2)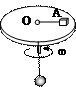

2.9 rad/s 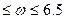 rad/s
rad/s
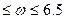 rad/s
rad/s要使B静止,A必须相对于转盘静止——具有与转盘相同的角速度.A需要的向心力由绳拉力和静摩擦力合成.角速度取最大值时,A有离心趋势,静摩擦力指向圆心O;角速度取最小值时,A有向心运动的趋势,静摩擦力背离圆心O.
对于B,T=mg
对于A,角速度取最大值时:
解得: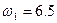 rad/s
rad/s
角速度取最小值时: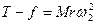
解得: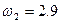 rad/s
rad/s
所以 2.9 rad/s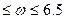 rad/s
rad/s
对于B,T=mg
对于A,角速度取最大值时:

解得:
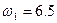 rad/s
rad/s 角速度取最小值时:
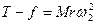
解得:
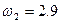 rad/s
rad/s所以 2.9 rad/s
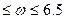 rad/s
rad/s 
练习册系列答案
相关题目
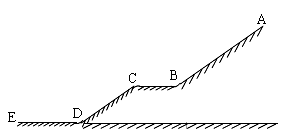

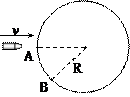
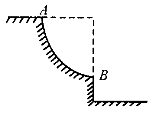
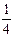 圆周,在B点轨道的切线是水平的,一质点自A点从静止开始下滑,不计摩擦和空气阻力,则在质点刚要到达B点时的加速度大小为 ,滑过B点时的加速度大小为 。
圆周,在B点轨道的切线是水平的,一质点自A点从静止开始下滑,不计摩擦和空气阻力,则在质点刚要到达B点时的加速度大小为 ,滑过B点时的加速度大小为 。