题目内容
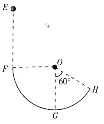
【题目】如图所示,一竖直放置半径为0.1m的光滑圆轨道,G为最低点,F点与圆心O等高,轨道右端H点与圆心连线与竖直方向夹角为60°,现从F点的正上方某处E点由静止释放一个质量为0.1kg的小球,进入圆轨道后,从H点飞出时的速度大小为2m/s。不计空气阻力,重力加速度g=10m/s2,下列说法正确的是
A.E、F间的竖直高度为0.12m
B.小球经过F点时对轨道压力的大小为0
C.小球从H点飞出后能上升的最大竖直高度为0.15m
D.小球从F点到G点的过程中所受重力的功率一直增大
【答案】C
【解析】
A.从E到H,由机械能守恒定律可得:
![]()
解得:
h=0.2m
由几何关系得:
![]() m
m
故A错误;
B.从E到F,由机械能守恒定律可得:
![]()
在F点,轨道对小球的弹力提供向心力,有:
![]()
联立解得:N=3N,由牛顿第三定律可知小球经过F点时对轨道压力的大小为3N,故B错误;
C.小球从H点飞出后竖直分速度为:
![]()
上升的最大竖直高度为:
![]() m
m
故C正确;
D.根据机械能守恒可知,小球的速率增大,在竖直方向的分速度先增大后减小,由
![]()
分析知小球b所受重力的功率先增大后减小,小球从F点到G点的过程中所受重力的功率先增大后减小,故D错误。

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目