Question

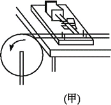
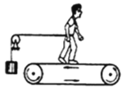
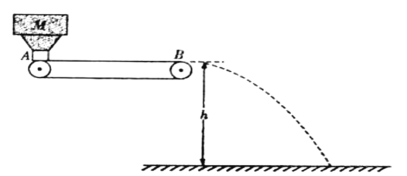
【题目】如图所示是工厂利用水平传送带传送小物料的装罝示意图.工作时，装置每隔相等的时间△t=0.35s释放规格相同的物料至传送带A 端（物料此时速度可忽略不计），物料随即被传送带送至B端并被水平抛出，落至地面后物料即被移走.已知传送带以恒定速率v=2.0m/s运行， A、B端距离L=1.8m，B端离地高度h=7.2m.物料与传送带间动摩擦因数μ=0.25.忽略空气的阻力，重力加速度g=10m/s2.求：

（1）物料从A端运动到B端的时间；

（2）当某个物料刚着地时，传送带B端右侧空中有多少个物料？

Answer 1

【答案】(1) t= 1.3s (2) n=3

【解析】

（1）假设物料在传送带上能加速至与传送带等速.设此过程的时间为t1、位移为s1.由牛顿运动定律和运动学方程有：

μmg=ma ①

v=at1 ②

由①②式可得：

t1=0. 8 s ③

有：s1=t1 ④

可得s1=0.8 m<L，所以物料在传送带上先做匀加速运动后做匀速运动.设物料匀速运动的时间为t2，有:

L-s1=vt2 ⑤

物料从A端运动到B端的时间：

t=t1+t2，⑥

由③④⑤⑥式并代入数据可得：

t= 1.3 s ⑦

（2）物料离开传送带B端后做平樾运动，设在空中运动的时间为t3，由平抛运动的规律有:

h= ⑧

设空中的物料最多有n个，由于物料每隔△t= 0. 35s释放，则有：

n≤ ⑨

由⑧⑨式并代入题给数据，解得：

n=3