��Ŀ����
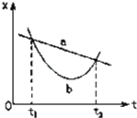
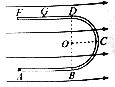
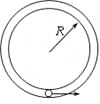
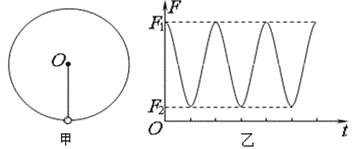
����Ŀ��һ�Ա����뾶ΪR���ܶȾ��ȵ�ij������棬������ʵ�飺�ò����쳤������˩һ����Ϊm��С���϶˹̶���O�㣬��ͼ����ʾ��������͵㴦��С��һ���ٶȣ�ʹ����O������ֱƽ������Բ���˶���ͨ����������¼������������СF��ʱ��t�ı仯������ͼ����ʾ����֪F1�Ĵ�С����7F2����������ΪG�������������ƣ��� ��
A.�����������������ٶ�Ϊ![]()
B.�����Ƹ�����ĵ�һ�����ٶ�Ϊ![]()
C.�����������Ϊ![]()
D.С��ͨ����ߵ����С�ٶ�Ϊ��
���𰸡�AC
��������
A������������͵�ʱϸ�ߵ�����ΪF1���ٶ�Ϊv1����
![]()
����������ߵ�ϸ�ߵ�����ΪF2���ٶ�Ϊv2����
![]()
�ɻ�е���غ㶨�ɵ�
mg2r+![]() mv22=
mv22=![]() mv12
mv12
���
![]()
��
F1=7F2
���Ը����������������ٶ�Ϊ
![]()
��A��ȷ��
B���������������ṩ��������
![]()
�����Ƹ�����ĵ�һ�����ٶ�Ϊ
![]()
��B����
C����������棬�����������Ƶ�������
![]()
���
![]()
��C��ȷ��
D��С������ߵ�����������������������ţ���˶����ɵ�
![]()
����С������ߵ����С��
![]()
��D����
��ѡAC��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ