Question

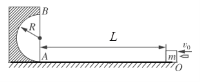
【题目】如图所示，半径为R0.4m，内壁光滑的半圆形轨道固定在水平地面上，质量m0.98kg的滑块停放在距轨道最低点A为L6m的O点处。质量为m00.02kg的子弹以速度v0400m/s从右边水平射入滑块，并留在其中．已知滑块与水平地面间的动摩擦因数0.4，子弹与滑块的作用时间很短．g10m/s2，求：

（1）子弹相对滑块静止时二者的共同速度大小v；

（2）滑块从O点滑到A点的时间t；

（3）通过计算分析滑块能否到达最高点B.

Answer 1

【答案】（1）（2）（3）由机械能守恒定律得，故不能

【解析】

（1）子弹击中滑块过程动量守恒，规定向左为正方向，
则：m0v0=（m+m0）v
代入数据解得：v=8m/s
（2）子弹击中滑块后与滑块一起在摩擦力的作用下向左作匀减速运动，设其加速度大小 为a，则：μ（m+m0）g=（m+m0）a…①
由匀变速运动的规律得：vt-at2=L…②
由①②并代入数据得：t=1s，（t=3s舍去）…③
（3）滑块从O点滑到A点时的速度vA=v-at，代入数据得：vA=4m/s
设滑块从A点滑上轨道后通过最高点B点时的速度vB，由机械能守恒定律：

（m+m0）vA2=（m+m0）g2R+（m+m0）vB2
代入数据得：vB=0< ，可知滑块不能到达B点；