题目内容
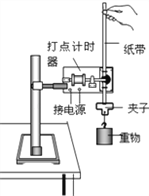
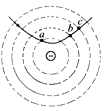
【题目】如图所示,在纸面内直线MN的左侧存在磁感应强度为B,方向垂直纸面向里的匀强磁场。在纸面内的整个空间还存在范围足够大的匀强电场,现有一个质量为m、电荷量为q的带正电粒子,以速度![]() 沿直线AP匀速运动,并从直线MN上的P点离开磁场。已知A点到直线MN的距离
沿直线AP匀速运动,并从直线MN上的P点离开磁场。已知A点到直线MN的距离![]() ,粒子重力不计。
,粒子重力不计。

(1)求匀强电场的场强大小和方向;
(2)粒子离开磁场后再次经过直线MN时到O点的距离;
(3)若粒子的初速度大小变为原来的一半,仍沿AP方向开始运动,此运动过程中粒子离开AP的最远距离![]() ,求此时粒子的速度大小及加速度大小。
,求此时粒子的速度大小及加速度大小。
【答案】(1)E=Bv0;方向垂直AP斜向上;(2)![]() (3)
(3)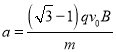
【解析】(1)粒子以速度v0沿直线AP匀速运动,说明电场力与洛伦兹力平衡,则:qE=qv0B
匀强电场的场强大小E=v0B;方向垂直AP斜向上;

(2)粒子离开磁场后,做类平抛,轨迹为PD,如图

因AO=PO,则θ=45°,PC=CD=v0t=![]() at2 ,
at2 , ![]()
再次经过直线MN时到O点的距离:DO=![]() PC+PO
PC+PO
由以上各式,得![]()
(3)若粒子的初速度大小变为原来的一半,轨迹如图,离开AP的最远距离为F,速度为![]()

粒子由A到F,由动能定理,得: ![]() ,
, ![]()
由上式,得: ![]()
![]() 由
由![]()
此时粒子的加速度大小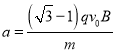

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目