题目内容
【题目】皮带运输机是靠货物和传送带之间的摩擦力把货物送往别处的，如图所示，已知传送带与水平面的倾角为θ=37°，以4m/s的速率向上匀速运行，在传送带的底端A处无初速度地放上一质量为0.5kg的物体，它与传送带间的动摩擦因数为0.8，若传送带底端A到顶端B的长度为24m，则物体从A到B的时间为多少？（取g=10m/s2，sin37°=0.6，物体与传送带间的最大静摩擦力等于它与传送带间的滑动摩擦力）
【答案】
【解析】试题分析：根据受力分析得到物体速度小于传送带时的加速度，进而由匀变速运动规律求得匀加速运动时间、位移，再根据受力分析得到之后的运动状态，根据匀加速运动或匀速运动的位移规律得到后一部分的运动时间，即可得到AB的运动时间．
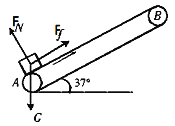
物体的受力情况如图所示. 
代入数值得
，可见
所以物体向上做匀加速运动，直到速度达到v=4m/s．
设经历的时间为t1，由牛顿第二定律得
，
解得
，则
，
解得t1=10s， 
，解得
当物体的速度为4m/s的瞬间，物体与传送带保持相对静止，由于物体与传送带间的最大静摩擦力为3.2N等于它与传送带间的滑动摩擦力）大于
，物体与传送带间存在相对的运动趋势，故物体受到向上的静摩擦力的作用，且
.
在剩下的路程s2=s-s1=4m里物体随传送带一起向上匀速运动， 
解得
．
物体从A端运动到B端的总时间为
．
名校课堂系列答案
【题目】某同学在研究性学习中记录了一些与地球、月球有关的数据资料如图中表所示，利用这些数据来计算地球表面与月球表面之间的距离s，则下列运算公式中错误的是（）
地球半径 | R=6400km |
月球半径 | r=1740km |
地球表面重力加速度 | g0=9.80m/s2 |
月球表面重力加速度 | g′=1.56m/s2 |
月球绕地球转动的线速度 | v=1km/s |
月球绕地球转动周期 | T=27.3天 |
光速 | c=2.998×105 km/s |
用激光器向月球表面发射激光光束，经过约t=2.565s接收到从月球表面反射回来的激光信号 | |
A. s=c
B. s=
﹣R﹣r
C. s=
﹣R﹣r D. s=
﹣R﹣r
