题目内容
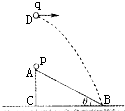 如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度L=2.5m,斜面倾角为θ=30°.不计空气阻力,g取10m/s2.求:
如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑.当小球p开始下滑时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度L=2.5m,斜面倾角为θ=30°.不计空气阻力,g取10m/s2.求:(1)小球p从A点滑到B点的时间;
(2)小球q抛出时初速度的大小和D点离地面的高度h.
分析:(1)根据牛顿第二定律求出P的加速度,结合位移时间公式求出小球P的运动时间.
(2)平抛运动在竖直方向上做自由落体运动,根据位移时间公式求出离地的高度.在水平方向上做匀速直线运动,结合水平位移和时间求出初速度的大小.
(2)平抛运动在竖直方向上做自由落体运动,根据位移时间公式求出离地的高度.在水平方向上做匀速直线运动,结合水平位移和时间求出初速度的大小.
解答:解:(1)设小球P从斜面上下滑的加速度为a,分析受力得:mgsinθ=ma
解得a=gsinθ=5m/s2.
设小球P从斜面上下滑的时间为t,L=
at2,
代入数据解得t=1s.
(2)小球q的运动为平抛运动:h=
gt2=5(m)
Lcosθ=v0t,
代入数据解得v0=
m/s.
答:(1)小球P从A点滑到B点的时间为1s.(2)小球q的初速度为
m/s,抛出点离地面的高度为5m.
解得a=gsinθ=5m/s2.
设小球P从斜面上下滑的时间为t,L=
| 1 |
| 2 |
代入数据解得t=1s.
(2)小球q的运动为平抛运动:h=
| 1 |
| 2 |
Lcosθ=v0t,
代入数据解得v0=
5
| ||
| 4 |
答:(1)小球P从A点滑到B点的时间为1s.(2)小球q的初速度为
5
| ||
| 4 |
点评:本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
 如图所示,斜面体的上表面除AB段粗糙外,其余部分光滑.一物体从斜面的顶端滑下,经过A、C两点时的速度相等,已知AB=BC,物体与AB段的动摩擦因数处处相等,斜面体始终静止在地面上,则( )
如图所示,斜面体的上表面除AB段粗糙外,其余部分光滑.一物体从斜面的顶端滑下,经过A、C两点时的速度相等,已知AB=BC,物体与AB段的动摩擦因数处处相等,斜面体始终静止在地面上,则( )| A、物体在AB段和BC段运动的加速度大小不相等 | B、物体在AB段和BC段运动的时间不相等 | C、物体在AB段和BC段运动时,斜面体受到地面静摩擦力的大小相等 | D、物体在AB段和BC段运动时,斜面体受到地面支持力的大小相等 |
 如图所示,斜面体ABC置于粗糙的水平地面上,小木块m在斜面上静止或滑动时,斜面体均保持静止不动.下列哪种情况,斜面体受到地面向右的静摩擦力?( )
如图所示,斜面体ABC置于粗糙的水平地面上,小木块m在斜面上静止或滑动时,斜面体均保持静止不动.下列哪种情况,斜面体受到地面向右的静摩擦力?( ) 如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑,当小球p开始下滑时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=2. 5m,斜面倾角为θ=30°.不计空气阻力,g取10m/s2.求:
如图所示,斜面体ABC固定在地面上,小球p从A点静止下滑,当小球p开始下滑时,另一小球q从A点正上方的D点水平抛出,两球同时到达斜面底端的B处.已知斜面AB光滑,长度l=2. 5m,斜面倾角为θ=30°.不计空气阻力,g取10m/s2.求: