题目内容
 如图所示,轻质弹簧的劲度系数为k,下面悬挂一个质量为m的砝码A,手持木板B托住A缓慢向上压弹簧,至某一位置静止.此时如果撤去B,则A的瞬时加速度为
如图所示,轻质弹簧的劲度系数为k,下面悬挂一个质量为m的砝码A,手持木板B托住A缓慢向上压弹簧,至某一位置静止.此时如果撤去B,则A的瞬时加速度为| 8 |
| 5 |
| 2 |
| 5 |
(1)砝码A能够做匀加速运动的时间?
(2)砝码A做匀加速运动的过程中,弹簧弹力对它做了多少功?木板B对它的支持力做了多少功?
分析:(1)弹簧初始是压缩的,末了是伸长的,依据加速度算出弹簧在初始状态的压缩量和末状态的伸长量,两者相加是物体匀加速运动的位移,在依据加速度可以求时间.
(2)因为有了压缩量和伸长量,可以求弹力的功,再用动能定理可以求木板弹力的功
(2)因为有了压缩量和伸长量,可以求弹力的功,再用动能定理可以求木板弹力的功
解答:(1)设初始状态弹簧压缩量为x1
则:kx1+mg=m×
g
解得:x1=
当B以a=
g匀加速向下运动时,由于a<g,所以弹簧在压缩状态时A、B不会分离,设该过程的终止时刻弹簧伸长量为x2
则:mg-kx2=m×
g
解得:x2=
A匀加速运动的位移s=x1+x2=
由位移关系式:s=
at2
解得:t=
(2)因为x1=x2
这一过程中弹簧对物体A的弹力做功为0
A、B分离时vA=at=
g
由动能定理得:mgs+WF=
mvA2
代入得:WF=-
答:
(1)砝码A能够做匀加速运动的时间为
(2)砝码A做匀加速运动的过程中,弹簧弹力对它做为零,木板B对它的支持力做为-
则:kx1+mg=m×
| 8 |
| 5 |
解得:x1=
| 3mg |
| 5k |
当B以a=
| 2 |
| 5 |
则:mg-kx2=m×
| 2 |
| 5 |
解得:x2=
| 3mg |
| 5k |
A匀加速运动的位移s=x1+x2=
| 6mg |
| 5k |
由位移关系式:s=
| 1 |
| 2 |
解得:t=
|
(2)因为x1=x2
这一过程中弹簧对物体A的弹力做功为0
A、B分离时vA=at=
| 2 |
| 5 |
|
由动能定理得:mgs+WF=
| 1 |
| 2 |
代入得:WF=-
| 18m2g2 |
| 25k |
答:
(1)砝码A能够做匀加速运动的时间为
|
(2)砝码A做匀加速运动的过程中,弹簧弹力对它做为零,木板B对它的支持力做为-
| 18m2g2 |
| 25k |
点评:本题一个难点是对物体匀加速末状态下受力的确定,由于A不受手的控制,因此在其只受重力和弹力而加速度为
g时,即是和B要分离的临界,之后就不再是匀加速运动了.
| 2 |
| 5 |

练习册系列答案
相关题目
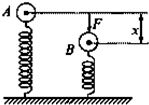 如图所示,轻质弹簧的劲度系数为k,小球重G,平衡时小球在A处,今用力F压小球至B处,使弹簧缩短x,则此时弹簧的弹力为( )
如图所示,轻质弹簧的劲度系数为k,小球重G,平衡时小球在A处,今用力F压小球至B处,使弹簧缩短x,则此时弹簧的弹力为( )| A、kx | B、kx+G | C、G-kx | D、以上都不对 |
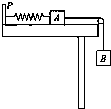 如图所示,轻质弹簧的一端固定在竖直板P上,另一端与质量为m1的物体A相连,物体A静止于光滑水平桌面上,A右边连接一细线绕过光滑的定滑轮悬挂一质量为m2的物体B(定滑轮的质量不计).开始时用手托住B,让细线恰好拉直,然后由静止释放B,直到B获得最大速度,下列有关此过程的分析正确的是( )
如图所示,轻质弹簧的一端固定在竖直板P上,另一端与质量为m1的物体A相连,物体A静止于光滑水平桌面上,A右边连接一细线绕过光滑的定滑轮悬挂一质量为m2的物体B(定滑轮的质量不计).开始时用手托住B,让细线恰好拉直,然后由静止释放B,直到B获得最大速度,下列有关此过程的分析正确的是( )| A、B物体机械能的减少量等于弹簧弹性势能与A物体动能的增加量之和 | B、A物体动能的增量等于细线拉力对A做的功 | C、B物体重力势能的减少量等于弹簧弹性势能的增加量 | D、A和B两物体的机械能之和一直保持不变 |
 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列说法正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列说法正确的是( ) 如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯在竖直方向运行时,电梯内乘客发现弹簧的伸长量比电梯静止时的伸长量小了,这一现象表明( )
如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯在竖直方向运行时,电梯内乘客发现弹簧的伸长量比电梯静止时的伸长量小了,这一现象表明( ) 如图所示,轻质弹簧的左端固定于竖直墙壁,右端悬空.一质量m=2.0kg的小球沿光滑水平地面以v0=4m/s的速度向左做匀速直线运动,碰撞轻质弹簧后原速离开弹簧.则:
如图所示,轻质弹簧的左端固定于竖直墙壁,右端悬空.一质量m=2.0kg的小球沿光滑水平地面以v0=4m/s的速度向左做匀速直线运动,碰撞轻质弹簧后原速离开弹簧.则: