题目内容
20.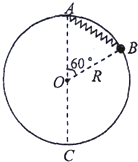 如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )| A. | 小球从B点滑到C点过程中,重力势能减少1.2mgR | |
| B. | 小球从B点滑到C点过程中,克服弹力做功kR2 | |
| C. | 小球经过C点时对环的作用力大小为mg+m$\frac{{{v}_{c}}^{2}}{R}$ | |
| D. | 小球从B到C的过程中,小球机械能减少1.5mgR-$\frac{1}{2}$mvc2 |
分析 小球由C到B的过程,由几何知识求出小球下降的高度,即可得到重力势能的减小量.求出在C点弹簧的弹性势能,即可求解克服弹力做功;小球在最低点C时,重力、弹簧的弹力和环对球的作用力提供向心力,写出方程,可求出环对小球的作用大小,从而得到小球对环的作用力大小.
解答 解:A、小球从B点滑到C点过程中,下降的高度为 h=Rcos60°+R=1.5R,则重力势能减少△Ep=mgh=1.5mgR,故A错误.
B、在C点时弹簧伸长量 x=R,弹性势能为Ep=$\frac{1}{2}k{x}^{2}$=$\frac{1}{2}k{R}^{2}$
所以小球由B到C的过程,克服弹力做功为$\frac{1}{2}k{R}^{2}$.故B错误.
C、小球经过C点时,有 N+kR-mg=m$\frac{{v}_{C}^{2}}{R}$,得N=mg+m$\frac{{{v}_{c}}^{2}}{R}$-kR,则小球经过C点时对环的作用力大小为mg+m$\frac{{{v}_{c}}^{2}}{R}$-kR,故C正确.
D、由机械能的概念知,小球从B到C的过程中,小球机械能减少1.5mgR-$\frac{1}{2}$mvc2.故D正确.
故选:D.
点评 该题中正确计算出重力和弹性势能是解题的关键.要知道弹簧的弹性势能表达式Ep=$\frac{1}{2}k{x}^{2}$,x是弹簧的形变量大小.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
10.有两人坐在椅子上休息,他们分别在中国的北京和郴州,关于他们具有的线速度和角速度相比较( )
| A. | 在郴州的人线速度大,在北京的人角速度大 | |
| B. | 在北京的人线速度大,在郴州的人角速度大 | |
| C. | 两处人的线速度和角速度一样大 | |
| D. | 两处人的角速度一样大,在郴州处人的线速度比在北京处人的线速度大 |
11.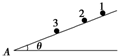 如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )
如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )
 如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )
如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )| A. | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{3}}{{t}_{3}}$ | B. | $\frac{{x}_{1}}{{t}_{1}}$>$\frac{{x}_{2}}{{t}_{2}}$>$\frac{{x}_{3}}{{t}_{3}}$ | ||
| C. | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$=$\frac{{x}_{2}}{{{t}_{2}}^{2}}$=$\frac{{x}_{3}}{{{t}_{3}}^{2}}$ | D. | 若θ增大,则$\frac{{x}_{1}}{{{t}_{1}}^{2}}$的值减小 |
15.下列说法正确的是( )
| A. | 液晶具有流动性 | |
| B. | 很大的物体一定不能看作质点 | |
| C. | 单向直线运动中位移就是路程 | |
| D. | 作用在任何一部分液面上的表面张力,总是跟这部分液面的分界线垂直 |
5.关于运动的合成和分解,下列说法正确的是( )
| A. | 合运动的方向就是物体实际运动的方向 | |
| B. | 已知两个分运动速度的大小,就可以确定合运动速度的大小 | |
| C. | 匀变速直线运动和匀速直线运动的合运动一定是曲线运动 | |
| D. | 若两匀速直线运动的速度大小分别为10m/s、5m/s,则合速度v大小的范围为5 m/s≤v≤15m/s |
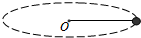 如图所示,细绳的一端固定于o点,另一端系一个小球.已知绳长0.4m,小球的质量为0.5kg.当小球在光滑水平面上以4rad/s的角速度做匀速圆周运动时,绳子的拉力为多大?
如图所示,细绳的一端固定于o点,另一端系一个小球.已知绳长0.4m,小球的质量为0.5kg.当小球在光滑水平面上以4rad/s的角速度做匀速圆周运动时,绳子的拉力为多大?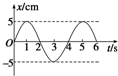 如图为一弹簧振子的振动图象,求:
如图为一弹簧振子的振动图象,求: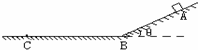 如图所示,斜面和水平面由一小段光滑圆弧连接,这样可以使得物体在B处改变运动方向时速度大小不变,斜面的倾角为37°,一质量为0.5kg的物块从距斜面底端B点5m处的A点由静止释放.已知物块与水平面和斜面的动摩擦因数均为0.3(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,斜面和水平面由一小段光滑圆弧连接,这样可以使得物体在B处改变运动方向时速度大小不变,斜面的倾角为37°,一质量为0.5kg的物块从距斜面底端B点5m处的A点由静止释放.已知物块与水平面和斜面的动摩擦因数均为0.3(sin37°=0.6,cos37°=0.8,g=10m/s2)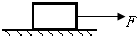 如图所示,在水平地面上有一质量为4.0kg的物块,它与地面间的动摩擦因数μ=0.2,在水平拉力F作用下,由静止开始运动.经过2.0s的时间物块发生了4.0m的位移.( g取10m/s2)
如图所示,在水平地面上有一质量为4.0kg的物块,它与地面间的动摩擦因数μ=0.2,在水平拉力F作用下,由静止开始运动.经过2.0s的时间物块发生了4.0m的位移.( g取10m/s2)