题目内容
11.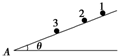 如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )
如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )| A. | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{3}}{{t}_{3}}$ | B. | $\frac{{x}_{1}}{{t}_{1}}$>$\frac{{x}_{2}}{{t}_{2}}$>$\frac{{x}_{3}}{{t}_{3}}$ | ||
| C. | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$=$\frac{{x}_{2}}{{{t}_{2}}^{2}}$=$\frac{{x}_{3}}{{{t}_{3}}^{2}}$ | D. | 若θ增大,则$\frac{{x}_{1}}{{{t}_{1}}^{2}}$的值减小 |
分析 小球在光滑斜面上释放时均做加速度大小为gsinθ的匀加速运动,由位移公式$x=\frac{1}{2}a{t}^{2}$求解x1、x2、x3与t1、t2、t3的关系.若增大θ,$\frac{x}{{t}^{2}}$的值增大.
解答 解:A、C:由于斜面是光滑的,故小球在斜面的受力如图: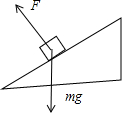
故小球在运动方向即沿斜面放下的受力为:F=mgsinθ,故小球的加速度为a=gsinθ,又小球由静止释放,初速度为零.位移公式$x=\frac{1}{2}a{t}^{2}$得:
解得:$\frac{x}{{t}^{2}}=\frac{1}{2}a$可见对三个小球来说,位移与时间平方的比值是一个定值,与其加速度成正比,而三个小球的加速度相同,故A错误.C正确;
B、某段时间内的平均速度$\overline{v}=\frac{x}{t}=\frac{v}{2}$,因为三个小球到达底端的速度v1>v2>v3,根据$\overline{v}=\frac{v}{2}$,可知平均速度$\overline{{v}_{1}}>\overline{{v}_{2}}>\overline{{v}_{3}}$所以,$\frac{{x}_{1}}{{t}_{1}}>\frac{{x}_{2}}{{t}_{2}}>\frac{{x}_{3}}{{t}_{3}}$,故B正确.
D、根据位移公式$x=\frac{1}{2}a{t}^{2}$得:$a=\frac{2x}{{t}^{2}}=gsinθ$,θ变大,则$\frac{x}{{t}^{2}}$的值增大,故D错误.
故选:BC.
点评 本题是位移公式$x=\frac{1}{2}a{t}^{2}$的应用,采用比例法研究.要掌握加速度大小为a=gsinθ.

练习册系列答案
相关题目
19.如图所示为一个质点作简谐振动的图象,在t1和t2时刻,质点的( )
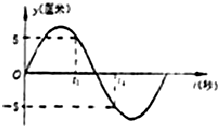

| A. | 加速度相同 | B. | 位移相同 | C. | 速度不相同 | D. | 回复力大小相同 |
6.下列说法正确的是( )
| A. | 分子间存在引力,使液体分子之间保持一定的间隙还不会分散开 | |
| B. | 气体的温度越高,某速率区间分子占总分子数的百分率一定越大 | |
| C. | 液晶分子没有固定的位置,但排列有大致相同的取向 | |
| D. | 蜘蛛网上挂着的小露珠呈球状属于毛细现象 |
16.若地球绕太阳公转周期及公转轨道半径分别为T和R,月球绕地球公转周期和公转轨道半径分别为t和r,则太阳质量与地球质量之比为( )
| A. | $\frac{{R}^{2}{t}^{3}}{{r}^{2}{T}^{3}}$ | B. | $\frac{{R}^{2}{T}^{3}}{{r}^{2}{t}^{3}}$ | C. | $\frac{{R}^{3}{T}^{2}}{{r}^{3}{t}^{2}}$ | D. | $\frac{{R}^{3}{t}^{2}}{{r}^{3}{T}^{2}}$ |
20.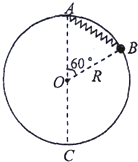 如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
 如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )| A. | 小球从B点滑到C点过程中,重力势能减少1.2mgR | |
| B. | 小球从B点滑到C点过程中,克服弹力做功kR2 | |
| C. | 小球经过C点时对环的作用力大小为mg+m$\frac{{{v}_{c}}^{2}}{R}$ | |
| D. | 小球从B到C的过程中,小球机械能减少1.5mgR-$\frac{1}{2}$mvc2 |
1.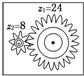 如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
 如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )| A. | 顺时针转动,周期为$\frac{2π}{3ω}$ | B. | 逆时针转动,周期为$\frac{2π}{3ω}$ | ||
| C. | 顺时针转动,周期为$\frac{6π}{ω}$ | D. | 逆时针转动,周期为$\frac{6π}{ω}$ |
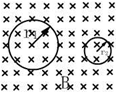 如图所示,均匀分布的磁场B,其磁感应强度随时间均匀变化,即B=Kt(K为常数),在磁场中有两个粗细相同的同种导线组成的圆环1和2,环面垂直于磁场,若两环的半径关系r1=2r2,则两环中产生的感应电流大小之比I1:I2是2:1.
如图所示,均匀分布的磁场B,其磁感应强度随时间均匀变化,即B=Kt(K为常数),在磁场中有两个粗细相同的同种导线组成的圆环1和2,环面垂直于磁场,若两环的半径关系r1=2r2,则两环中产生的感应电流大小之比I1:I2是2:1.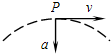
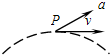
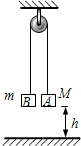 如图所示,一根细绳绕过光滑的定滑轮,两端分别系住A、B两物体,其质量M和m分别为0.6kg和0.4kg,开始时用手托住A,使A、B处于同一高度,离地高度h为1m,重力加速度g取10m/s2,设绳足够长,绳与滑轮的质量不计,求:
如图所示,一根细绳绕过光滑的定滑轮,两端分别系住A、B两物体,其质量M和m分别为0.6kg和0.4kg,开始时用手托住A,使A、B处于同一高度,离地高度h为1m,重力加速度g取10m/s2,设绳足够长,绳与滑轮的质量不计,求: