题目内容
10.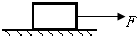 如图所示,在水平地面上有一质量为4.0kg的物块,它与地面间的动摩擦因数μ=0.2,在水平拉力F作用下,由静止开始运动.经过2.0s的时间物块发生了4.0m的位移.( g取10m/s2)
如图所示,在水平地面上有一质量为4.0kg的物块,它与地面间的动摩擦因数μ=0.2,在水平拉力F作用下,由静止开始运动.经过2.0s的时间物块发生了4.0m的位移.( g取10m/s2)试求:(1)物体的加速度大小;
(2)拉力F的大小.
分析 根据匀变速直线运动的位移时间公式求出物体的加速度,结合牛顿第二定律求出拉力F的大小.
解答 解:(1)设物体以加速度a做匀加速直线运动,
根据$x=\frac{1}{2}a{t}^{2}$得,
加速度a=$\frac{2x}{{t}^{2}}=\frac{2×4}{4}=2m/{s}^{2}$.
(2)取物体为研究对象进行受力分析
根据牛顿第二定律得,Fcos30°-μmg=ma
代入数据解得F=16N.
答:(1)物体的加速度大小为2m/s2;
(2)拉力F的大小为16N
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
20.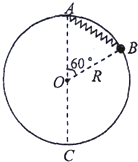 如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
 如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )
如图所示,竖直平面内固定一半径为R的粗糙圆环,A处固定一轻质弹簧,弹簧末端栓接一质量为m的小球B,小球套在圆环上.已知弹簧的原长也为R,劲度系数为k,将小球从图示位置由静止释放,小球将沿圆环滑动并通过最低点C,到达C点时小球速度为vc.下列说法正确的是( )| A. | 小球从B点滑到C点过程中,重力势能减少1.2mgR | |
| B. | 小球从B点滑到C点过程中,克服弹力做功kR2 | |
| C. | 小球经过C点时对环的作用力大小为mg+m$\frac{{{v}_{c}}^{2}}{R}$ | |
| D. | 小球从B到C的过程中,小球机械能减少1.5mgR-$\frac{1}{2}$mvc2 |
1.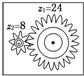 如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
 如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )| A. | 顺时针转动,周期为$\frac{2π}{3ω}$ | B. | 逆时针转动,周期为$\frac{2π}{3ω}$ | ||
| C. | 顺时针转动,周期为$\frac{6π}{ω}$ | D. | 逆时针转动,周期为$\frac{6π}{ω}$ |
5.分子间的引力和斥力都与分子间的距离有关,下列说法正确的是( )
| A. | 无论分子间的距离怎样变化,分子间的引力和斥力总是相等的 | |
| B. | 无论分子间的距离怎样变化,分子间的斥力总小于引力 | |
| C. | 当分子间的引力增大时,斥力一定减小 | |
| D. | 当分子间的距离增大时,分子间的斥力比引力减小得快 |
15.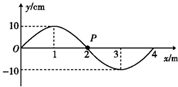 如图所示为一列简谐横波在t=0时的波形图,此时介质中的质点P沿y轴正方向运动,其振动周期为0.4s则( )
如图所示为一列简谐横波在t=0时的波形图,此时介质中的质点P沿y轴正方向运动,其振动周期为0.4s则( )
 如图所示为一列简谐横波在t=0时的波形图,此时介质中的质点P沿y轴正方向运动,其振动周期为0.4s则( )
如图所示为一列简谐横波在t=0时的波形图,此时介质中的质点P沿y轴正方向运动,其振动周期为0.4s则( )| A. | 波沿x轴负方向传播 | |
| B. | 波的传播速度为10m/s | |
| C. | 质点P的振幅为20cm | |
| D. | 质点P在一个周期内沿波传播方向移动了4m |
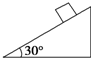 如图所示,一质量为1.2kg的物体从倾角为30°、长度为10m的光滑斜面顶端由静止开始下滑.物体滑到斜面底端时重力做功的瞬时功率是多少?整个过程中重力做功的平均功率是多少?(g取10m/s2)
如图所示,一质量为1.2kg的物体从倾角为30°、长度为10m的光滑斜面顶端由静止开始下滑.物体滑到斜面底端时重力做功的瞬时功率是多少?整个过程中重力做功的平均功率是多少?(g取10m/s2)