Question

【题目】如图所示，在斜面上有四条光滑细杆。其中OA杆竖直放置，0B杆与 0D杆等长，0C杆与斜面垂直放置，每根杆上都套着一个小滑环（图中未画出），四个环分别从0点由静止释放，沿OA、OB、0C、0D滑到斜面上所用的时间依次为t1、t2、t3、t4下列关系正确的是（ ）

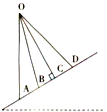
A、t1＞t2B、t1=t3C、t2=t4D、t2＜t4

Answer 1

【答案】ABD

【解析】试题分析：以OA为直径画圆，如图，

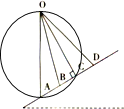
根据等时圆模型，对小滑环，受重力和支持力，将重力沿杆的方向和垂直杆的方向正交分解，根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为：（θ为杆与竖直方向的夹角），由图中的直角三角形可知，小滑环的位移：，所以，t与θ无关，

可知从圆上最高点沿任意一条弦滑到底所用时间相同，故沿OA和OC滑到底的时间相同，即t1=t3，OB不是一条完整的弦，时间最短，即t1＞t2，OD长度超过一条弦，时间最长，即t2＜t4，故选ABD。