题目内容
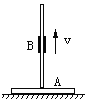
【题目】如图所示,一质量m=65kg的选手参加“挑战极限运动”,要在越过宽度s=3m的水沟后跃上高h=1.8m的平台。他采用的方法是:手握长L=3.05m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直(不弯曲),人的重心恰好位于杆的顶端,此刻人放开杆水平飞出,最终落到平台上(重心恰在平台表面)。不计运动过程中的空气阻力,已知该选手匀加速运动的距离SAB=16m,到达B点时速度vB=8m/s,人跑动过程中重心离地高度H=1.0m取g=10m/s2,求选手
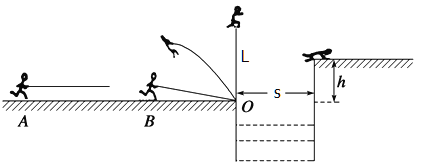
(1)匀加速助跑的动力F;
(2)在最高点的最小速度v;
(3)在B点蹬地弹起瞬间,人做功的最小值W。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)在匀加速助跑阶段,由动能定理得: FSAB=![]() mvB2﹣0,故F=
mvB2﹣0,故F=![]() =130N。
=130N。
(2)设人在最高点速度为v,人离开杆后做平抛运动,有:
竖直方向有:L﹣h=![]() gt2
gt2
水平方向有:![]()
解得:v= s![]() =6m/s 。
=6m/s 。
即人要最终到达平台,在最高点飞出时刻的速度应至少为![]() 。
。
(3)在人蹬地到最高点过程,由动能定理得:W﹣mg(L﹣H)=![]() mv2-
mv2-![]() mvB2
mvB2
解得 ![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目