题目内容
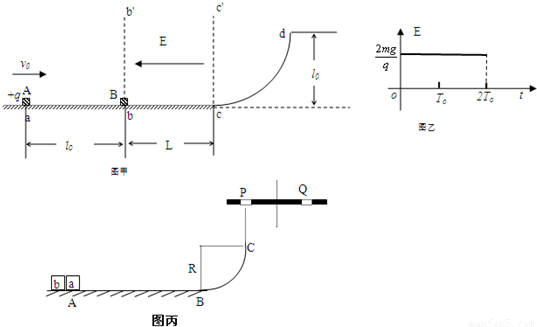
A.如图甲所示,质量为m的不带电绝缘小物块B静止在b点,绝缘水平轨道abc与绝缘光滑圆弧轨道cd平滑连接,d为cd轨道的最高点.质量为m、电量为+q的小物块A以初速度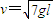 自a点开始水平向右运动,到达b点与小物块B发生正碰,碰撞后A、B粘合在一起不再分离.与此同时,在分界面bb'与分界面cc'之间的空间内附加一水平向左的电场,设小物块AB进入电场时为t=0时刻,电场随时间变化的图象如图乙所示,已知场强
自a点开始水平向右运动,到达b点与小物块B发生正碰,碰撞后A、B粘合在一起不再分离.与此同时,在分界面bb'与分界面cc'之间的空间内附加一水平向左的电场,设小物块AB进入电场时为t=0时刻,电场随时间变化的图象如图乙所示,已知场强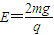 ,
,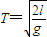 ,a、b两点距离为l,电场的宽度为
,a、b两点距离为l,电场的宽度为 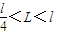 ,d点高度为l,小物块A、B与水平轨道的动摩擦因数μ=0.5,其余摩擦不计,小物块A、B均视为质点.重力加速度用g表示.求:
,d点高度为l,小物块A、B与水平轨道的动摩擦因数μ=0.5,其余摩擦不计,小物块A、B均视为质点.重力加速度用g表示.求:(1)小物块A到达b点即将与小物块B碰撞前的速度vA大小.
(2)自小物块A从a点开始运动到小物块A、B第一次离开电场,试讨论在这个过程中摩擦力对小物块A、B做的总功Wf与L的关系
(3)判断小物块AB能否上滑到cd轨道的d点.
B.如图丙所示,a、b两滑块原来紧靠在一起,静止在水平面上的A点,滑块a、b的质量分别为m、2m,物块与水平地面间的动摩擦因数为0.1,B点为圆轨道的最低点,A、B之间的距离为5R.现在a、b在某种内力的作用下突然分开,a以
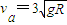 的速度由A点开始向B点滑行,并滑上光滑的半径为R的
的速度由A点开始向B点滑行,并滑上光滑的半径为R的  圆弧BC,在C点正上方有一离C点高度也为R的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q,旋转时两孔均能达到C点的正上方.若滑块滑过C点后从P孔上升又恰能从Q孔落下,求
圆弧BC,在C点正上方有一离C点高度也为R的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q,旋转时两孔均能达到C点的正上方.若滑块滑过C点后从P孔上升又恰能从Q孔落下,求(1)分开后b球获得的速度vb
(2)滑块a在B点时对轨道的压力;
(3)滑块上升至P点时的速度vP
(4)平台转动的角速度ω应满足什么条件?
【答案】分析:解A的难点是假设两滑块碰后在电场中速度减为零时求出发生的位移S及时间t,再将在电场中运动总时间与2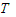 做比较,从而做出讨论.B的难点在于滑块滑过C点后从P孔上升又恰能从Q孔落下Q转过的角度满足θ=π,π+2π=3π,π+4π=5π…,即可写出θ=(2n+1)π表达式,然后θ=ωt求解.
做比较,从而做出讨论.B的难点在于滑块滑过C点后从P孔上升又恰能从Q孔落下Q转过的角度满足θ=π,π+2π=3π,π+4π=5π…,即可写出θ=(2n+1)π表达式,然后θ=ωt求解.
解答:解:A、(1)小物块A从a点滑到b点,动能定理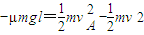
得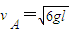
即小物块A到达b点即将与小物块B碰撞前的速度vA大小为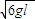
(2)A、B碰撞,设碰后速度为v,动量守恒定律mvA=2mv
得: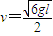
AB一起在电场减速运动,设速度为0时,位移为S,动能定理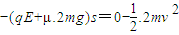
将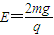 代入得:
代入得: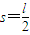
对向右减速过程有 qE+μ.2mg=2ma1 得: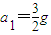
减速为0所用时间为: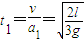
对向左加速过程有 qE-μ.2mg=2ma2 得: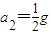
由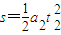 可得到达左边界bb'的时间:
可得到达左边界bb'的时间: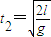
所以在电场中最长运动时间: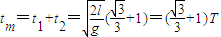 因tm<2T,即小物块AB在bb'与cc'之间运动时,一直受到电场力作用.
因tm<2T,即小物块AB在bb'与cc'之间运动时,一直受到电场力作用.
讨论如下:
①当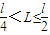 时,L≤s,AB可以穿过电场右边界cc',
时,L≤s,AB可以穿过电场右边界cc',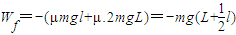
②当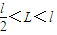 时,L>s,AB在电场先向右做减速运动,速度减为0,由于qE=2mg>f=mg,即AB最后向左加速,从左边界bb'离开电场.则
时,L>s,AB在电场先向右做减速运动,速度减为0,由于qE=2mg>f=mg,即AB最后向左加速,从左边界bb'离开电场.则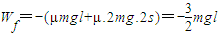
即当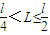 时
时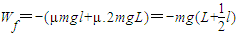
当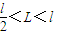 时
时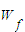 =-
=-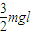
(3)①当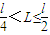 ,AB穿越电场的右边界cc',设到达c的动能为EKc
,AB穿越电场的右边界cc',设到达c的动能为EKc
由动能定理: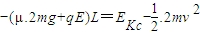
得: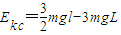
即: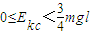
由于 Ekc<2mgl,不能到达d点.
②当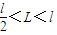 时,AB从左边界bb'离开电场,不能到达d点.
时,AB从左边界bb'离开电场,不能到达d点.
即
B.解:
(1)a、b分开的过程,选向右方向为正方向,由动量守恒得mva-2mvb=0
解之得: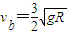
(2)设滑块至B点时速度为vB,对滑块由A点到B点应用动能定理有: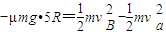
对滑块在B点,由牛顿第二定律有: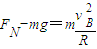
解得:FN=9mg
由牛顿第三定律可知,滑块在B点时对轨道的压力大小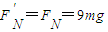 方向竖直向下.
方向竖直向下.
(3)滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vP,则: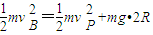
解得: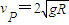
(4)滑块穿过P孔后再回到平台的时间:t=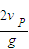 =4
=4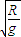
要想实现题述过程,需满足:ωt=(2n+1)π
解得: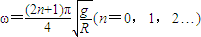
点评:求解物理题的关键还是物理过程的分析,根据不同的物理过程建立物理模型列式求解.
 做比较,从而做出讨论.B的难点在于滑块滑过C点后从P孔上升又恰能从Q孔落下Q转过的角度满足θ=π,π+2π=3π,π+4π=5π…,即可写出θ=(2n+1)π表达式,然后θ=ωt求解.
做比较,从而做出讨论.B的难点在于滑块滑过C点后从P孔上升又恰能从Q孔落下Q转过的角度满足θ=π,π+2π=3π,π+4π=5π…,即可写出θ=(2n+1)π表达式,然后θ=ωt求解.解答:解:A、(1)小物块A从a点滑到b点,动能定理
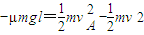
得
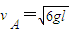
即小物块A到达b点即将与小物块B碰撞前的速度vA大小为
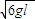
(2)A、B碰撞,设碰后速度为v,动量守恒定律mvA=2mv
得:
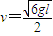
AB一起在电场减速运动,设速度为0时,位移为S,动能定理
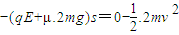
将
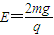 代入得:
代入得: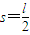
对向右减速过程有 qE+μ.2mg=2ma1 得:
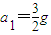
减速为0所用时间为:
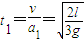
对向左加速过程有 qE-μ.2mg=2ma2 得:
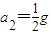
由
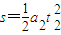 可得到达左边界bb'的时间:
可得到达左边界bb'的时间: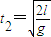
所以在电场中最长运动时间:
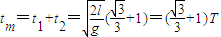 因tm<2T,即小物块AB在bb'与cc'之间运动时,一直受到电场力作用.
因tm<2T,即小物块AB在bb'与cc'之间运动时,一直受到电场力作用.讨论如下:
①当
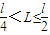 时,L≤s,AB可以穿过电场右边界cc',
时,L≤s,AB可以穿过电场右边界cc',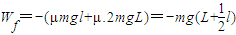
②当
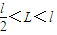 时,L>s,AB在电场先向右做减速运动,速度减为0,由于qE=2mg>f=mg,即AB最后向左加速,从左边界bb'离开电场.则
时,L>s,AB在电场先向右做减速运动,速度减为0,由于qE=2mg>f=mg,即AB最后向左加速,从左边界bb'离开电场.则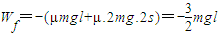
即当
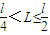 时
时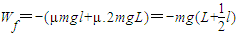
当
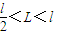 时
时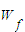 =-
=-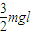
(3)①当
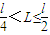 ,AB穿越电场的右边界cc',设到达c的动能为EKc
,AB穿越电场的右边界cc',设到达c的动能为EKc由动能定理:
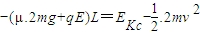
得:
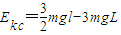
即:
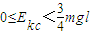
由于 Ekc<2mgl,不能到达d点.
②当
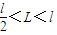 时,AB从左边界bb'离开电场,不能到达d点.
时,AB从左边界bb'离开电场,不能到达d点.即
B.解:
(1)a、b分开的过程,选向右方向为正方向,由动量守恒得mva-2mvb=0
解之得:
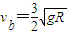
(2)设滑块至B点时速度为vB,对滑块由A点到B点应用动能定理有:
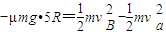
对滑块在B点,由牛顿第二定律有:
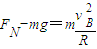
解得:FN=9mg
由牛顿第三定律可知,滑块在B点时对轨道的压力大小
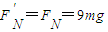 方向竖直向下.
方向竖直向下.(3)滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vP,则:
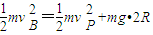
解得:
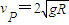
(4)滑块穿过P孔后再回到平台的时间:t=
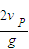 =4
=4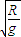
要想实现题述过程,需满足:ωt=(2n+1)π
解得:
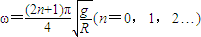
点评:求解物理题的关键还是物理过程的分析,根据不同的物理过程建立物理模型列式求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
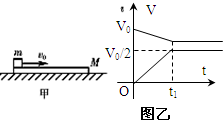 如图甲所示,质量为M的木板静止在光滑水平面上,一个质量为m的小滑块以初速度υ0从木板的左端向右滑上木板.滑块和木板速度随时间变化的图象如图乙所示,某同学根据图象作出如下一些判断,正确的是( )?
如图甲所示,质量为M的木板静止在光滑水平面上,一个质量为m的小滑块以初速度υ0从木板的左端向右滑上木板.滑块和木板速度随时间变化的图象如图乙所示,某同学根据图象作出如下一些判断,正确的是( )?
 如图甲所示,质量为m=0.5kg,初速度v0=10m/s的物体,受到一个与初速度v0方向相反的外力F作用,沿粗糙的水平面滑动,物体与地面间的动摩擦因数为μ,经3s后撤去外力,直到物体停止.整个过程物体的v-t图象如图乙所示 (g=10m/s2). 则( )
如图甲所示,质量为m=0.5kg,初速度v0=10m/s的物体,受到一个与初速度v0方向相反的外力F作用,沿粗糙的水平面滑动,物体与地面间的动摩擦因数为μ,经3s后撤去外力,直到物体停止.整个过程物体的v-t图象如图乙所示 (g=10m/s2). 则( )