题目内容
18. 一个卫星绕着某一星球作匀速圆周运动,轨道半径为R1,因在运动过程中与宇宙尘埃和小陨石的摩擦和碰撞,导致该卫星发生跃迁,轨道半径减小为R2,如图所示,则卫星的线速度、角速度,周期的变化情况是( )
一个卫星绕着某一星球作匀速圆周运动,轨道半径为R1,因在运动过程中与宇宙尘埃和小陨石的摩擦和碰撞,导致该卫星发生跃迁,轨道半径减小为R2,如图所示,则卫星的线速度、角速度,周期的变化情况是( )| A. | v增大,ω增大,T减小 | B. | v减小,ω增大,T增大 | ||
| C. | v增大,ω减小,T增大 | D. | v减小,ω减小,T减小 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、向心加速度和向心力的表达式进行讨论即可.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有F=F向,
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=mω2r=m$\frac{{4π}^{2}}{{T}^{2}}$r
求得v=$\sqrt{\frac{GM}{r}}$,ω=$\sqrt{\frac{GM}{{r}^{3}}}$,T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,
根据v=$\sqrt{\frac{GM}{r}}$可知,轨道半径减小,线速度增大;
根据ω=$\sqrt{\frac{GM}{{r}^{3}}}$可知,轨道半径减小,角速度增大;
根据T=2π$\sqrt{\frac{{r}^{3}}{GM}}$可知,轨道半径减小,周期减小;
故选:A
点评 本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、向心加速度和向心力的表达式,再进行讨论.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
20. 如图所示为某一匀强电场,两极板距离为10cm,两极板间电压为100V,其中A距正极板2cm,B距负极板2cm,AB长为12cm,以下说法中正确的是( )
如图所示为某一匀强电场,两极板距离为10cm,两极板间电压为100V,其中A距正极板2cm,B距负极板2cm,AB长为12cm,以下说法中正确的是( )
 如图所示为某一匀强电场,两极板距离为10cm,两极板间电压为100V,其中A距正极板2cm,B距负极板2cm,AB长为12cm,以下说法中正确的是( )
如图所示为某一匀强电场,两极板距离为10cm,两极板间电压为100V,其中A距正极板2cm,B距负极板2cm,AB长为12cm,以下说法中正确的是( )| A. | A点的电势为20V | B. | B点的电势为20V | ||
| C. | AB两点间电势差为60V | D. | AB两点间电势差为80V |

 在做“研究匀变速直线运动”的实验时,得到一条纸带如图所示,A、B、C、D、E、F、G为计数点,每两个计数点间还有4个点未画出,x1=1.20cm,x2=1.60cm,x3=2.00cm,x4=2.40cm,x5=2.80cm,x6=3.20cm
在做“研究匀变速直线运动”的实验时,得到一条纸带如图所示,A、B、C、D、E、F、G为计数点,每两个计数点间还有4个点未画出,x1=1.20cm,x2=1.60cm,x3=2.00cm,x4=2.40cm,x5=2.80cm,x6=3.20cm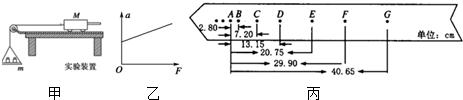
 如图所示,一质量m=4.0kg的物体,由高h=2.0m、倾角θ=53°的固定斜面顶端滑到底端.物体与斜面间的动摩擦因数为μ=0.2.求;
如图所示,一质量m=4.0kg的物体,由高h=2.0m、倾角θ=53°的固定斜面顶端滑到底端.物体与斜面间的动摩擦因数为μ=0.2.求;
 如图所示,是示波器工作原理的示意图,电子经电压U1从静止加速后垂直进入偏转电场,偏转电场的电压为U2,两极板间距为d,极板长度为L,电子离开偏转电场时的偏转量为h,每单位电压引起的偏转量($\frac{h}{{U}_{2}}$)叫示波器的灵敏度.下列方法可以提高示波器的灵敏度的是( )
如图所示,是示波器工作原理的示意图,电子经电压U1从静止加速后垂直进入偏转电场,偏转电场的电压为U2,两极板间距为d,极板长度为L,电子离开偏转电场时的偏转量为h,每单位电压引起的偏转量($\frac{h}{{U}_{2}}$)叫示波器的灵敏度.下列方法可以提高示波器的灵敏度的是( ) 在“用打点计时器测速度”的实验中,小车拖着纸带运动,打出的纸带如图所示.选出A、B、C、D、E共5个计数点,每相邻两点间还有四个计时点(图中未画出),以A点为起点量出的到各点的位移已标在图上.由此可求得打下B点时小车运动的速度约为vB=0.17m/s;打下D点时小车运动的速度约为vD=0.21m/s.(结果保留二位有效数字)
在“用打点计时器测速度”的实验中,小车拖着纸带运动,打出的纸带如图所示.选出A、B、C、D、E共5个计数点,每相邻两点间还有四个计时点(图中未画出),以A点为起点量出的到各点的位移已标在图上.由此可求得打下B点时小车运动的速度约为vB=0.17m/s;打下D点时小车运动的速度约为vD=0.21m/s.(结果保留二位有效数字)