题目内容
 已知一足够长斜面倾角为θ=37°,一质量m=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤去力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
已知一足够长斜面倾角为θ=37°,一质量m=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤去力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:(1)物体与斜面间的动摩擦因数μ;
(2)从撤去力F开始2秒末物体的速度v.
(3)从撤去力F开始多长时间后物体回到斜面体的底部.
分析:(1)物体先沿斜面向上做匀加速运动,撤去F后做匀减速运动.根据运动学公式求出前2s内物体的加速度,由牛顿第二定律和摩擦力公式求出物体与斜面间的动摩擦因数μ;
(2)由牛顿第二定律求出撤去F后物体的加速度,由速度公式求出撤去F开始2s末物体的速度v.
(3)根据牛顿第二定律求出撤去F后物体的加速度,由运动学公式求解物体在斜面上运动的最大位移.由牛顿第二定律和运动学公式结合求出物体下滑的时间.抓住上滑与下滑的位移大小相等.
(2)由牛顿第二定律求出撤去F后物体的加速度,由速度公式求出撤去F开始2s末物体的速度v.
(3)根据牛顿第二定律求出撤去F后物体的加速度,由运动学公式求解物体在斜面上运动的最大位移.由牛顿第二定律和运动学公式结合求出物体下滑的时间.抓住上滑与下滑的位移大小相等.
解答:解:(1)设物体在前2s内的加速度大小为a1,由x1=
a1
得
a1=
=2m/s2
物体匀加速运动的过程中,受到重力mg、斜面的支持力N、摩擦力f和拉力F,根据牛顿第二定律得
F-f-mgsin37°=ma1
又f=μN=μmgcos37°
代入解得,μ=0.25
(2)撤去F后,物体继续向上做匀减速运动,当速度减小到零时,物体的位移达到最大值.设这个过程中物体的加速度大小为a2,位移大小为x2,时间为t2,刚撤去F时物体的速度大小为v1,则有v1=a1t1=4m/s
根据牛顿第二定律得:
f+mgsin37°=ma2
解得a2=8m/s2
则t2=
=0.5s,
由02-v12=-2a2x2得
x2=
=1m
所以从开始运动起,物体在斜面上运动的最大位移为x=x1+x2=5m.
由于μ<tan37°,故物体将从最高点下滑.
设下滑的加速度大小为a3,则
mgsin37°-μmgcos37°=ma3,
解得,a3=4m/s2,从撤去力F开始2秒末物体的速度v=a3t3=4×1.5=6m/s
(3)从最高点到斜面底部所用的时间为t4,则有
x=
a3
代入解得,t4=
s≈1.56s
故从撤去力F开始物体回到斜面体的底部所用的时间为t′=t2+t4=2.16s.
答:(1)物体与斜面间的动摩擦因数μ是0.25;
(2)从撤去力F开始2秒末物体的速度v是6m/s.
(3)从撤去力F开始2.16s时间后物体回到斜面体的底部.
| 1 |
| 2 |
| t | 2 1 |
a1=
| 2x1 | ||
|
物体匀加速运动的过程中,受到重力mg、斜面的支持力N、摩擦力f和拉力F,根据牛顿第二定律得
F-f-mgsin37°=ma1
又f=μN=μmgcos37°
代入解得,μ=0.25
(2)撤去F后,物体继续向上做匀减速运动,当速度减小到零时,物体的位移达到最大值.设这个过程中物体的加速度大小为a2,位移大小为x2,时间为t2,刚撤去F时物体的速度大小为v1,则有v1=a1t1=4m/s
根据牛顿第二定律得:
f+mgsin37°=ma2
解得a2=8m/s2
则t2=
| v1 |
| a2 |
由02-v12=-2a2x2得
x2=
| ||
| 2a2 |
所以从开始运动起,物体在斜面上运动的最大位移为x=x1+x2=5m.
由于μ<tan37°,故物体将从最高点下滑.
设下滑的加速度大小为a3,则
mgsin37°-μmgcos37°=ma3,
解得,a3=4m/s2,从撤去力F开始2秒末物体的速度v=a3t3=4×1.5=6m/s
(3)从最高点到斜面底部所用的时间为t4,则有
x=
| 1 |
| 2 |
| t | 2 4 |
代入解得,t4=
| ||
| 2 |
故从撤去力F开始物体回到斜面体的底部所用的时间为t′=t2+t4=2.16s.
答:(1)物体与斜面间的动摩擦因数μ是0.25;
(2)从撤去力F开始2秒末物体的速度v是6m/s.
(3)从撤去力F开始2.16s时间后物体回到斜面体的底部.
点评:本题运用牛顿第二定律和运动学公式结合求解动力学问题,要学会分析过程,把握住各个过程之间的联系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图所示,已知一足够长斜面倾角为θ=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤销力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,已知一足够长斜面倾角为θ=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤销力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: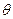 =37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: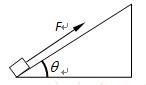
 ;
;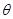 =37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: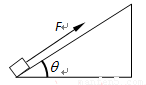
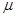 ;
;