题目内容
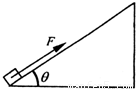
 如图所示,已知一足够长斜面倾角为θ=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤销力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,已知一足够长斜面倾角为θ=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤销力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:(1)物体与斜面间的动摩擦因数μ;
(2)从撤销力F开始2秒末物体的速度v.
分析:(1)物体先沿斜面向上做匀加速运动,撤去F后做匀减速运动.根据运动学公式求出前2s内物体的加速度,由牛顿第二定律和摩擦力公式求出物体与斜面间的动摩擦因数μ;
(2)由牛顿第二定律求出撤去F后物体的加速度,由速度公式求出撤去F开始2s末物体的速度v.
(2)由牛顿第二定律求出撤去F后物体的加速度,由速度公式求出撤去F开始2s末物体的速度v.
解答:解:(1)设力F作用时物体的加速度为a1,t1=2s,
则由s=
a1
得:a1=
=
=2m/s2
有力F作用时,由牛顿第二定律得:F-mgsinθ-μmgcosθ=ma1
代入数据可求得:μ=0.25
(2)设撤销力F的瞬间物体的速度为v1,则v1=a1t1=4m/s
设撤销力F以后,物体沿斜面减速上滑的加速度为a2,依牛顿第二定律有:
mgsinθ+μmgcosθ=ma2 得:a2=8m/s2
设从撤销力F至达最高点历时t2,由v=at得:t2=
=0.5s,
设物体达最高点后沿斜面加速下滑的加速度为a3,
则由mgsinθ-μmgcosθ=ma3得a3=4m/s2
加速下滑时间 t3=t-t2=1.5s
故撤销力F后2s末物体的速度为v=a3t3=6m/s,方向沿斜面向下
答:(1)物体与斜面间的动摩擦因数μ为0.25;
(2)从撤销力F开始2秒末物体的速度v为6m/s,方向沿斜面向下.
则由s=
| 1 |
| 2 |
| t | 2 1 |
| 2s | ||
|
| 2×4 |
| 22 |
有力F作用时,由牛顿第二定律得:F-mgsinθ-μmgcosθ=ma1
代入数据可求得:μ=0.25
(2)设撤销力F的瞬间物体的速度为v1,则v1=a1t1=4m/s
设撤销力F以后,物体沿斜面减速上滑的加速度为a2,依牛顿第二定律有:
mgsinθ+μmgcosθ=ma2 得:a2=8m/s2
设从撤销力F至达最高点历时t2,由v=at得:t2=
| v1 |
| a2 |
设物体达最高点后沿斜面加速下滑的加速度为a3,
则由mgsinθ-μmgcosθ=ma3得a3=4m/s2
加速下滑时间 t3=t-t2=1.5s
故撤销力F后2s末物体的速度为v=a3t3=6m/s,方向沿斜面向下
答:(1)物体与斜面间的动摩擦因数μ为0.25;
(2)从撤销力F开始2秒末物体的速度v为6m/s,方向沿斜面向下.
点评:本题运用牛顿第二定律和运动学公式结合求解动力学问题,要学会分析过程,把握住各个过程之间的联系.

练习册系列答案
相关题目
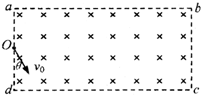 一足够长的矩形区域abcd内充满磁感应强度为B,方向垂直纸面向里的匀强磁场,矩形区域的左边界ad宽为L,现从ad中点O垂直于磁场射入一带电粒子,速度大小为v0方向与ad边夹角为30°,如图所示.已知粒子的电荷量为q,质量为m(重力不计).
一足够长的矩形区域abcd内充满磁感应强度为B,方向垂直纸面向里的匀强磁场,矩形区域的左边界ad宽为L,现从ad中点O垂直于磁场射入一带电粒子,速度大小为v0方向与ad边夹角为30°,如图所示.已知粒子的电荷量为q,质量为m(重力不计).
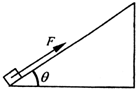 如图所示,已知一足够长斜面倾角为θ=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤销力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,已知一足够长斜面倾角为θ=37°,一质量M=10kg物体,在斜面底部受到一个沿斜面向上的F=100N的力作用由静止开始运动,物体在2秒内位移为4m,2秒末撤销力F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: