题目内容
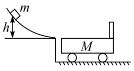
一辆装有砂子的小车,总质量M="10" kg,以速度v0="2" m/s沿光滑水平直轨运动.有一质量m="2" kg的铁球以速度v="7" m/s投入小车内的砂子中,求下列各种情况下,铁球投入后小车的速度.
(1)铁球迎面水平投入;
(2)铁球从后面沿车行方向投入;
(3)铁球由小车上方竖直向下投入.
(1)铁球迎面水平投入;
(2)铁球从后面沿车行方向投入;
(3)铁球由小车上方竖直向下投入.
(1)0.5 m/s.
(2)2.83 m/s.
(3)1.67 m/s.
(2)2.83 m/s.
(3)1.67 m/s.
选砂车和铁球组成的系统为研究对象,在铁球进入砂车的过程中,水平方向不受外力作用,水平方向动量守恒,规定车行方向(v0的方向)为正方向.
(1)设铁球迎面水平投入后,铁球与砂车的共同速度为v1,根据动量守恒定律有:
Mv0-mv=(m+M)v1,v1= =
=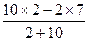 m/s="0.5" m/s.
m/s="0.5" m/s.
(2)设铁球从后面沿车行方向投入后,铁球与砂车的共同速度为v2,根据动量守恒定律有:
Mv0+mv=(m+M)v2,v2= =
= m/s="2.83" m/s.
m/s="2.83" m/s.
(3)设铁球竖直向下投入砂车后,铁球与砂车的共同速度为v3,根据动量守恒定律有:
Mv0+0=(m+M)v3,解得:v3=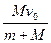 =
= m/s="1.67" m/s.
m/s="1.67" m/s.
(1)设铁球迎面水平投入后,铁球与砂车的共同速度为v1,根据动量守恒定律有:
Mv0-mv=(m+M)v1,v1=
 =
=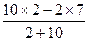 m/s="0.5" m/s.
m/s="0.5" m/s.(2)设铁球从后面沿车行方向投入后,铁球与砂车的共同速度为v2,根据动量守恒定律有:
Mv0+mv=(m+M)v2,v2=
 =
= m/s="2.83" m/s.
m/s="2.83" m/s.(3)设铁球竖直向下投入砂车后,铁球与砂车的共同速度为v3,根据动量守恒定律有:
Mv0+0=(m+M)v3,解得:v3=
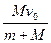 =
= m/s="1.67" m/s.
m/s="1.67" m/s.
练习册系列答案
相关题目


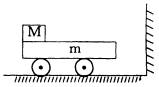
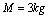 的小滑块,滑块与平板车之间的摩擦系数。开始时平板车和滑块以
的小滑块,滑块与平板车之间的摩擦系数。开始时平板车和滑块以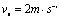 的速度在光滑平面上向右运动,并与竖直墙发生碰撞,设碰撞时间极短,且碰撞后平板车速度大小保持不变,但方向与原来相反。平板车足够长,以至滑块不会滑到平板车右端。(取
的速度在光滑平面上向右运动,并与竖直墙发生碰撞,设碰撞时间极短,且碰撞后平板车速度大小保持不变,但方向与原来相反。平板车足够长,以至滑块不会滑到平板车右端。(取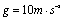 )求:
)求: