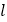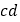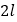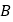题目内容
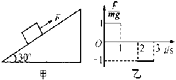
【题目】如图甲所示,在倾角为300的足够长的光滑斜面上,有一质量为m的物体,受到沿斜面方向的力F作用,力F按图乙所示的规律变化, 图中纵坐标是F与mg的比值,规定力沿斜面向上为正向,则物体运动的速度v随时间t变化的规律用可图中的哪一个图象表示(物体的初速度为零)
A. 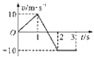 B.
B. 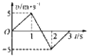
C. 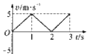 D.
D. 
【答案】D
【解析】试题分析:在0-1s内,通过受力分析由牛顿第二定律可得:F-mgsin30°=ma1
解得:a1=0.5g=5m/s
1s末获得速度为:v1=a1t1=5m/s
在1-2s内,由牛顿第二定律可得:-mgsin30°=ma2
解得:a2=0.5g=5m/s2
向上做减速运动,2s末的速度为:v2=v1+a2t2=0
在2-3s内由牛顿第二定律得:-F-mgsin30°=ma3
解得:a3=-1.5g=15m/s
3s末获得速度为:v3=a3t3=-15m/s
故D正确;故选D.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
【题目】某十字路口的监控录像显示,一辆汽车在马路上行驶,t=0时,汽车在十字路口中心的左侧20m处;过了2s,汽车正好到达十字路口的中心;再过3s,汽车行驶到了十字路口中心右侧30m处.如果把这条马路抽象为一条坐标轴x,十字路口中心定为坐标轴的原点,向右为x轴的正方向.

(1)试将汽车在三个观测时刻的位置坐标填入表中.
观测 时刻 | t=0时 | 过2s | 再过3s |
位置 坐标 | x1= | x2= | x3= |
(2)说出前2s内、后3s内汽车的位移分别为多少?这5s内的位移又是多少?